 Use the slope formula to show that all four sides are perpendicular.
To show that the line from (-1,0) to (2,3) is perpendicular
to the the line segment from (2,3) to (5,0),
1. find the slope of the line segment from
(-1,0) to (2,3):
Use the slope formula:
Use the slope formula to show that all four sides are perpendicular.
To show that the line from (-1,0) to (2,3) is perpendicular
to the the line segment from (2,3) to (5,0),
1. find the slope of the line segment from
(-1,0) to (2,3):
Use the slope formula:


 where (x1,y1) = (-1,0)
and where (x2,y2) = (2,3)
where (x1,y1) = (-1,0)
and where (x2,y2) = (2,3)


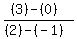


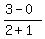





 2. find the slope of the line segment from
(2,3) to (5,0):
Use the slope formula:
2. find the slope of the line segment from
(2,3) to (5,0):
Use the slope formula:


 this time where (x1,y1) = (2,3)
and where (x2,y2) = (5,0)
this time where (x1,y1) = (2,3)
and where (x2,y2) = (5,0)


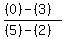





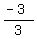


 3. Point out that their slopes 1 and -1, are
opposite-signed reciprocals, or what is the
same thing, their product (1)(-1) is -1. That
proves that they are perpendicular and that the
angle between them is a right angle.
4. Find the length of the line segment from
(-1,0) to (2,3):
Use the distance formula:
3. Point out that their slopes 1 and -1, are
opposite-signed reciprocals, or what is the
same thing, their product (1)(-1) is -1. That
proves that they are perpendicular and that the
angle between them is a right angle.
4. Find the length of the line segment from
(-1,0) to (2,3):
Use the distance formula:


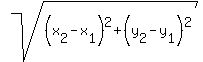 where (x1,y1) = (-1,0)
and where (x2,y2) = (2,3)
where (x1,y1) = (-1,0)
and where (x2,y2) = (2,3)








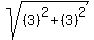


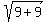


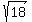


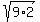


 5. Find the length of the line segment from
(2,3) to (5,0):
Use the distance formula:
5. Find the length of the line segment from
(2,3) to (5,0):
Use the distance formula:


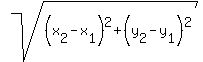 this time where (x1,y1) = (2,3)
and where (x2,y2) = (5,0)
this time where (x1,y1) = (2,3)
and where (x2,y2) = (5,0)


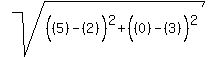








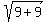


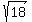


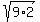


 6. Point out that the two line segments are equal
in length.
Now, using the same method, finish by showing that
the slope of the line segment from (5,0) to (2,-3)
is perpendicular to the line segment from (2,3) to
(5,0). Then show that those line segments are
equal in length.
Then show that the slope of the line segment from
(5,0) to (2,-3) is perpendicular to the line segment
from (2,-3) to (-1,0). Then show that those line
segments are equal in length.
Then point out that the line segment from (2,-3) to
(-1,0) is perpendicular to the line segment from
(-1,0) to (2,3), and that is has the same length.
You finish.
Edwin
6. Point out that the two line segments are equal
in length.
Now, using the same method, finish by showing that
the slope of the line segment from (5,0) to (2,-3)
is perpendicular to the line segment from (2,3) to
(5,0). Then show that those line segments are
equal in length.
Then show that the slope of the line segment from
(5,0) to (2,-3) is perpendicular to the line segment
from (2,-3) to (-1,0). Then show that those line
segments are equal in length.
Then point out that the line segment from (2,-3) to
(-1,0) is perpendicular to the line segment from
(-1,0) to (2,3), and that is has the same length.
You finish.
Edwin