Implicit differentiation is done when the derivative y' is to
be found from an equation involving y which cannot be or has
not been, solved for y.
The important thing to remember is that although the derivative
of x is 1, the derivative of y is y', not 1, and we always must
remember to use the chain rule.



We will need these formulas:
(1) 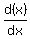

 (2)
(2) 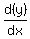

 (3)
(3) 

 (4)
(4) 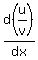




 We use (3) to differentiate the left side, and for the
chain rule, we use (4). On the right we use (1) and (2):
We use (3) to differentiate the left side, and for the
chain rule, we use (4). On the right we use (1) and (2):
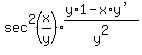

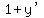 All that's left is to solve for y':
Drop the *1 by the y:
All that's left is to solve for y':
Drop the *1 by the y:


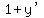 Multiply both sides by y² to clear the fraction:
Multiply both sides by y² to clear the fraction:


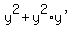 Distribute
Distribute  into the parentheses (y-x*y') on the left
into the parentheses (y-x*y') on the left


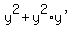 Get all the terms that contain y' on the right and
get other terms on the right:
Get all the terms that contain y' on the right and
get other terms on the right:
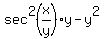

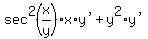 Factor out y' on the right
Factor out y' on the right
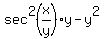

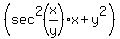 Divide both sides by
Divide both sides by 


 Edwin
Edwin