Question 1050687: Please help me solved this math now. Find the equation of
a circle tangent to the line 2x - 3y = -7 at (1,3) passing
through (11, 1).
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Pls help me solved this math now. Find the equation of a circle target to the line 2× - 3¶ = -7 at (1,3) passing through (11, 1).
----------
I'll assume you mean tangent, but it's still not clear.
-----
2× - 3¶ = -7 ???
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The red line is the given line 2x-3y = -7,
The green and blue lines are radii of the circle.
We need the slope of the given red line so we can get
the equation of the green line, which is perpendicular
to it:
2x-3y = 7
-3y = -2x+7
  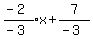
   <--equation of red line
Comparing to y = mx+b, slope of red line = <--equation of red line
Comparing to y = mx+b, slope of red line =  The green line is perpendicular to the red line, so
the green line's slope is the negative reciprocal of
The green line is perpendicular to the red line, so
the green line's slope is the negative reciprocal of
 which is which is  .
The green line passes through (1,3), so we use the point-
slope formula to find its equation .
The green line passes through (1,3), so we use the point-
slope formula to find its equation
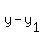  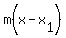
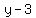   clear fraction by multiplyng through by 2
clear fraction by multiplyng through by 2
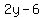  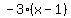
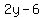  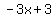
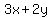   <-- eq. of the green line
The center of the circle (h,k) is a point on
the green line, so we substitute (x,y) = (h,k)
eq. 1: <-- eq. of the green line
The center of the circle (h,k) is a point on
the green line, so we substitute (x,y) = (h,k)
eq. 1: 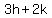   We use the distance formula to find an expression
for the length of the green and blue lines, which
will be the radius, so
We use the distance formula to find an expression
for the length of the green and blue lines, which
will be the radius, so
    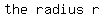 Square both sides:
Square both sides:
  
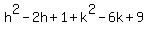  
   Simplify by cancelling h2's and k2's
Simplify by cancelling h2's and k2's
  
   Divide through by 4
Divide through by 4
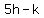  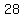 So we put this with equation (1) above
as a system of equations:
So we put this with equation (1) above
as a system of equations:
 Solve that system by substitution and get
(h,k) = (5,-3) <-- center of circle
We find the radius from
Solve that system by substitution and get
(h,k) = (5,-3) <-- center of circle
We find the radius from
    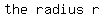
  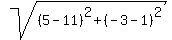  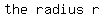
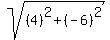  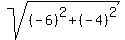  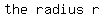
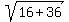  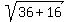  
     So the radius is
So the radius is  Equation of circle:
Equation of circle:
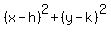  
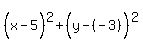  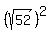
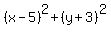   Edwin
Edwin
|
|
|