Question 1050528: Flying with the wind, a plane flew 1200 mi in 5 h. Against the wind, the plane required 6 h to fly the same distance. Find the rate of the plane in calm air and the rate of the wind
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Flying with the wind, a plane flew 1200 mi in 5 h. Against the wind, the plane required 6 h to fly the same distance.
Find the rate of the plane in calm air and the rate of the wind
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
From the condition, you have these two equations
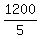 = u + v, (1) (flying with wind, the equation for the speed) = u + v, (1) (flying with wind, the equation for the speed)
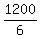 = u - v. (2) (flying against the wind)
Here u is the plane speed at no wind, v is the wind speed.
Simplify the system (1), (2):
u + v = 240, (3)
u - v = 200. (4)
To solve it, add the equations (3) and (4). You will get
2u = 240 + 200 ---> 2u = 440 ---> u = = u - v. (2) (flying against the wind)
Here u is the plane speed at no wind, v is the wind speed.
Simplify the system (1), (2):
u + v = 240, (3)
u - v = 200. (4)
To solve it, add the equations (3) and (4). You will get
2u = 240 + 200 ---> 2u = 440 ---> u = 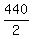 = 220.
You just found the speed of the plane at no wind. It is 220 mph.
Now you can easily find v from (1): v = 240 - u = 240 - 220 - 20.
Thus the speed of the wind is 20 mph.
Answer. Speed of the plane at no wind is 220 mph. The speed of the wind is 20 mph. = 220.
You just found the speed of the plane at no wind. It is 220 mph.
Now you can easily find v from (1): v = 240 - u = 240 - 220 - 20.
Thus the speed of the wind is 20 mph.
Answer. Speed of the plane at no wind is 220 mph. The speed of the wind is 20 mph.
For more similar problems and more details related to solutions see the lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Wind and Current problems solvable by quadratic equations
- Selected problems from the archive on the boat floating Upstream and Downstream
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Travel and Distance problems" of the section "Word problems".
|
|
|