SOLUTION: Prove that if k is an integer then (4k+1)i^4k + (4k+2)i^4k+1 + (4k+3)i^4k+2 + (4k+4)i^4k+3= 2-2i. Use this to prove that 1+2i+3i^2+4i^3+...+1995i^1994+1996i^1995=-998-998i

Algebra ->  Equations -> SOLUTION: Prove that if k is an integer then (4k+1)i^4k + (4k+2)i^4k+1 + (4k+3)i^4k+2 + (4k+4)i^4k+3= 2-2i. Use this to prove that 1+2i+3i^2+4i^3+...+1995i^1994+1996i^1995=-998-998i      Log On


   

Question 1050433: Prove that if k is an integer then (4k+1)i^4k + (4k+2)i^4k+1 + (4k+3)i^4k+2 + (4k+4)i^4k+3= 2-2i.
Use this to prove that
1+2i+3i^2+4i^3+...+1995i^1994+1996i^1995=-998-998i
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
i%5E%284k%29+=+%28i%5E4%29%5Ek+=+1%5Ek+=+1
===>i%5E%284k%2B1%29+=+i,
i%5E%284k%2B2%29+=+-1, and
i%5E%284k%2B3%29+=+-i.
===>
=
= -2+-+2i.

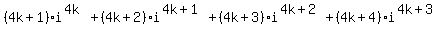
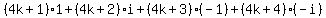
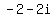Now substitute the values of k = 0, 1, 2, 3,...,497, 498 into the formula.
On the left side of the equation, we would get
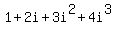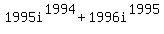1%2B2i%2B3i%5E2%2B4i%5E3+...+1995i%5E1994%2B1996i%5E1995,
while on the right side, we would get
499*(-2 - 2i) = -998 - 998i.
Therefore,
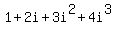1%2B2i%2B3i%5E2%2B4i%5E3+...+1995i%5E1994%2B1996i%5E1995+=+-998-998i.