Question 1049882: Find the distance between the lines 2x-2y+3z-12=0=2x+2y+z , 2x-z=0=5x-2y+9
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2x-2y+3z-12 = 0 = 2x+2y+z represent the line that is the intersection of the two planes 2x-2y+3z-12 = 0 and 2x+2y+z = 0. Similarly, 2x-z = 0 = 5x-2y+9 represent the intersection of the planes 2x-z = 0 and 5x-2y+9 = 0.
In the first pair of planes, solving for x and y in terms of z gives x + z = 3 and y - z/2 = -3. The symmetric equation of the line of intersection is thus  . This line . This line  has direction vector < -1,1/2,1 >, or < -2,1,2 > with the fraction cleared, and passes through the point (3,-3,0). has direction vector < -1,1/2,1 >, or < -2,1,2 > with the fraction cleared, and passes through the point (3,-3,0).
The second pair of planes would give a line of intersection with symmetric equation  , with direction vector < 1/2, 5/4,1 >, or < 2,5,4 > with the fractions cleared. This line , with direction vector < 1/2, 5/4,1 >, or < 2,5,4 > with the fractions cleared. This line  line passes through the point (0,9/2,0). line passes through the point (0,9/2,0).
The vector 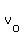 starting at the point (0,9/2,0) of starting at the point (0,9/2,0) of  and terminating at the point (3,-3,0) of and terminating at the point (3,-3,0) of  is given by < 3,-15/2,0 >, or < 6,-15,0 >, with the fraction cleared. is given by < 3,-15/2,0 >, or < 6,-15,0 >, with the fraction cleared.
Now a vector N perpendicular to both the direction vectors of the two intersection lines is < 1,-2,2 >. (This can be obtained either by getting the cross product of the two direction vectors, or by solving simultaneously the system < a,b,c >*< -2,1,2 > = 0 and < a,b,c >*< 2,5,4 > = 0 for a,b, and c.)
The distance between the two lines is then just the scalar projection of the vector 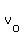 onto the vector N: onto the vector N:
 . .
|
|
|