Question 1049719: In a class of 100 people, 25 own fords, 20 own dodges, 13 own toyotas, 10 own both fords and dodges, 8 own fords and toyotas, 5 own dodges and toyotas, and 4 own all three. If a person selected at random from the class, what is the probability he or she does not own any of these vehicles? Use a venn diagram.
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a class of 100 people, 25 own fords, 20 own dodges, 13 own toyotas, 10 own both fords and dodges, 8 own fords and toyotas, 5 own dodges and toyotas, and 4 own all three. If a person selected at random from the class, what is the probability he or she does not own any of these vehicles? Use a venn diagram.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Similar problem was solved in
https://www.algebra.com/statistics/Binomial-probability/Binomial-probability.faq.question.1048656.html
https://www.algebra.com/statistics/Binomial-probability/Binomial-probability.faq.question.1048656.html
Apply the same logic.
The numbers are
100 - [25 + 20 + 13 - (10 + 8 + 5) + 4] = 61.
So, the number of people in the class who does not own any of these vehicles is 61.
Therefore, the answer to the question is 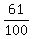 . .
The formula we used is well known in the elementary set theory.
Its proof is very straightforward and simple.
See, for example, the lesson
- Advanced problems on counting elements in sub-sets of a given finite set
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook in the topic "Miscellaneous word problems" of the section "Word problems".
|
|
|