SOLUTION: The distinct real numbers x and y satisfy x^2=33y+907 and y^2=33x+907. Find x and y.

x^2 = 33y + 907,   (1)
y^2 = 33x + 907.   (2)

Distract eq.(2) from eq.(1) (both sides). You will get

x^2 - y^2 = 33y - 33x,   or

(x-y)*(x+y) = -33(x-y).

Since the numbers are distinct, you can divide both sides of the last equation by (x-y). Then you get

x + y = -33.        (3)

Now express  x = -33-y from (3) and substitute it into (2). You will get

y^2 = 33(-33-y) + 907,   or

y^2 + 33y + 182 = 0.

Solve this quadratic equation using the quadratic formula.

 =  = ,

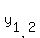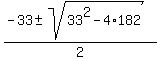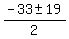 = -7,   = -26.

Correspondingly, there are two solutions for x:

 = -33 - (-7) = -33 + 7 = -26,  and   = -33  (-26) = -33 + 26 = -7.

Answer.  The solutions are (x,y) = (-7,-26)  or/and (-26,-7).