Question 1049425: a polynomial f(x) with rational coefficients leaves remainder 15 when divided by x-3 and remainder 2x+1 when divided by (x-1)^2. Find the remainder when f(X) is divided by (x-3)(x-1)^2.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since divisor  is a polynomial of degree 3, the remainder we look for is a polynomial whose degree is at most 2. is a polynomial of degree 3, the remainder we look for is a polynomial whose degree is at most 2.
Let us say that remainder is  , and we have to find coefficients , and we have to find coefficients  , ,  , and , and  . .
So, 
Since the remainder is  when divided by when divided by  , ,  , so , so




When  is divided by is divided by 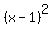 the remainder is the remainder of dividing the remainder is the remainder of dividing  by by  . .
That remainder is  . .
Since the polynomials  and and 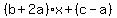 are the same polynomial, are the same polynomial,
 <---> <--->  . .
Along with the equation  highlighted above, we have the system of linear equations highlighted above, we have the system of linear equations
 . .
Substituting into the top equation the expressions for  and and  from the bottom two equations, we get from the bottom two equations, we get






 , and substituting , and substituting  for for  in the bottom two equations of the system, we get in the bottom two equations of the system, we get
   , and , and
  . .
So, it turns out that the remainder  that we were looking for is that we were looking for is
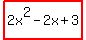 . .
|
|
|