SOLUTION: Tangent (theta) + square root of 3 = secant (theta) I tried squaring both sides but in the end I never result with the correct answer. I'm not sure how to start this one or wh

So, you are trying to solve an equation

tan(x) +  = sec(x).

It is the same as

 +  = .

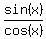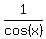Multiply both sides by cos(x). You will get

 +  = 1.


Multiply both sides by . You will get

 +  = .


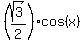Recall that  = ,   = .

Therefore, you can write the last equation as 

 = .


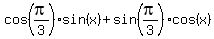Apply the addition formula for sine.  ( It is cos(a)*sin(b) + sin(a)*cos(b) = sin(a+b). 
                                        See the lesson Addition and subtraction formulas in this site ). You will get

 = .

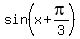It implies 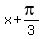  =   or   = .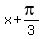

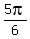Hence,  x = 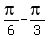 =  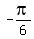 or  x =  =  = .

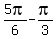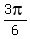The last root doesn't fit due to "sec" in the original equation.


Answer.  x = 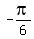,  or 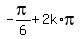  for any integer "k".