Question 1049296: A quantitative variable has 10 observations that have a median value of 15. The maximum of the 10 observations was recorded incorrectly and is changed from a value of 25 to a value of 30. The value of the new median is?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i believe the median will be unchanged.
the median is the middle term of the set of numbers after they have been ordered in ascending order from left to right.
you have 10 observations.
the middle term is (10 + 1)/2 = 11/2 = 5.5.
the means the median is between the 5th and 6th term.
the maximum value in the set of numbers has no bearing on the median.
it will be the same regardless of the value of the max term.
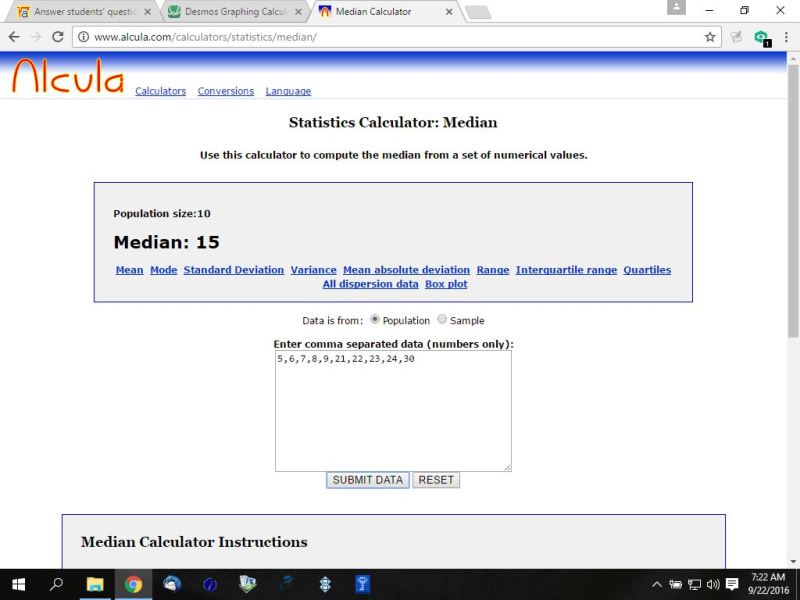
i created a set of data that has a maximum value of 25 with a median of 15.
that set of data is:
5, 6, 7, 8, 9, 21, 22, 23, 24, 25
i used a median calculator to find the median.
the median was 15.
i then changed the maximum value of the same data from 25 to 30 and used the median calculator again.
the median was 15.
this is because the median tells you that 50% of the numbers are below that value and 50% of the numbers are above that value.
the fact that the maximum value changed was irrelevant because 50% of the value were still above that same value.
here's a good reference on how to calculate mean, median, mode, and range.
http://www.purplemath.com/modules/meanmode.htm
here are the result from the median calculator i used.

|
|
|