Question 1049042: A rental truck and a car are traveling toward each other on the highway and are 220 miles apart. If the car is traveling 20 miles per hour faster than the rental truck and they pass after 2 hours, how fast is each vehicle traveling?
Found 3 solutions by advanced_Learner, ikleyn, MathTherapy:
Answer by advanced_Learner(501)   (Show Source):
Answer by ikleyn(52852)  (Show Source):
You can put this solution on YOUR website! .
A rental truck and a car are traveling toward each other on the highway and are 220 miles apart.
If the car is traveling 20 miles per hour faster than the rental truck and they pass after 2 hours, how fast is each vehicle traveling?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The governing equation is
C*2 + (C-20)*2 = 220,
where C is the car' speed in mph, and C-20 is the track' speed.
Simplifying, you have
(2C-20)*2 = 220,
2C - 20 = 110, ( =  )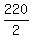
2C = 130,
C =  = 65 mph.
Thus you got the car' speed. It is 65 mph.
Then the track' speed is 65 - 20 = 45 mph.
Answer. The car' speed is 65 mph. The track' speed is 45 mph.
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
A rental truck and a car are traveling toward each other on the highway and are 220 miles apart. If the car is traveling 20 miles per hour faster than the rental truck and they pass after 2 hours, how fast is each vehicle traveling?
|
|
|
