Question 1048965: Hi
in a textbook the following problem was as follows.james has some matchsticks and sachets. If one matchstick is put into each sachet there are 2 matchsticks left.if he puts 2 matchsticks into each sachet he will have 24 sachets left. The solutions are m-s = 2 and s-m/2 = 24.
Can u help me understand how these equations were derived.
thank you
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hi
in a textbook the following problem was as follows. James has some matchsticks and sachets.
If one matchstick is put into each sachet there are 2 matchsticks left.
If he puts 2 matchsticks into each sachet he will have 24 sachets left.
The solutions are m-s = 2 and s-m/2 = 24.
Can u help me understand how these equations were derived.
thank you
~~~~~~~~~~~~~~~~~~~~~~~~~
There is no need to explain the first equation.
It is the direct and literal math translation of the condition
("If one matchstick is put into each sachet there are 2 matchsticks left.")
Regarding the second equation, firstly, the condition clearly assumes and means that the number of matchsticks is even.
Secondly, the number of sachets containing exactly 2 matchsticks is 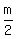 . The remaining s - . The remaining s - 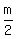 sachets are without matchsticks, and their number is 24,
in accordance with the condition.
It is exactly what the second equation says. sachets are without matchsticks, and their number is 24,
in accordance with the condition.
It is exactly what the second equation says.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let m equal the number of matchsticks.
let s equal the number of sachets.
first verbal statement:
if one matchstick is put into each sachet, there are 2 matchsticks left.
in order for this to occur, you have to have 2 more matchsticks than sachets.
your equation is therefore m = s + 2.
subtract s from both sides of this equation to get m - s = 2.
second verbal statement:
if 2 matchsticks are put in each sachet, there are 24 sachets left.
in order for this to occur, you have to have 24 more sachets than half the number of marbles.
the equation for this is therefore s = m/2 + 24.
subtract m/2 from both sides of this equation to get s - m/2 = 24.
another way these can be derived which is a little more difficult to understand is as follows:
when you put one matchstick into each sachet, you are left with 2 matchsticks.
this is like a division.
you are dividing the number of sachets by the number of matches and your result is 1 with a remainder of 2.
in a division, this is shown as s/m = 1 + 2/m
the remainder is really the fraction of what's left over divided by the divisor.
so you start with s/m = 1 + 2/m
then you multiply both sides of the equation by m to get s = m + 2
then you subtract m from both sides of the equation to gets - m = 2.
the second one is a little trickier but should give you the correct result if you do it right.
the statement says that if you put 2 matchsticks in each sachet, then you have 24 sachets left.
this means that is you divide the number of sachets by the number of marbles, your result will be 1/2 + a remainder of 24 sachets.
the algebraic equation for this would be s/m = 1/2 + 24/m.
multiply both sides of this equation by m and you get s = 1/2 * m + 24
subtract 1/2 * m from both sides of this equation to get s - 1/2 * m = 24
this can be shown as s - m/2 = 24.
from these two equations, you can solve for the number of sachets and the number of marbles.
the two equations are:
m - s = 2
s - m/2 = 24
solve for m in the first equation to get m = s + 2
replace m with s + 2 in the second equation to get:
s - (s+2)/2 = 24
multiply both sides of this equation by 2 to get 2s - (s+2) = 48
simplify to get 2s - s - 2 = 48
combine like terms to get s - 2 = 48
add 2 to both sides of this equation to get s = 50
since m = s + 2, then m = 52.
your solution is:
m = 52
s = 50
your first equation of m = s + 2 is satisfied because 52 = 50 + 2.
your second equation of s - m/2 = 24 is satisfied because 50 - 52/2 = 50 - 26 = 24.
both equations are satisfied so the value of m must be 52 and the value of s must be 50.
best i can do.
hopefully it makes sense to you.
first equations wasn't that hard to derive.
second equation took a little more thought.
|
|
|