SOLUTION: Hi there, I could use some help on this please! Assume that you toss a fair six-faced die two times. (a) (1 pt) How many possible outcomes are in the sample space? Expla

Algebra ->  Probability-and-statistics -> SOLUTION: Hi there, I could use some help on this please! Assume that you toss a fair six-faced die two times. (a) (1 pt) How many possible outcomes are in the sample space? Expla      Log On


   

Question 1048822: Hi there, I could use some help on this please!
Assume that you toss a fair six-faced die two times.

(a) (1 pt) How many possible outcomes are in the sample space? Explain your answer.

(b) (1 pt) What is the probability that you get a number greater than 3 at the first toss? (Show work and write the answer in simplest fraction form)


(c) (2 pts) What is the probability that the sum of the two tosses is at least 9? (Show work and write the answer in simplest fraction form)


(d) (2 pts) What is the probability that the sum of the two tosses is at least 9, given that you get a number greater than 3 in the first toss? (Show work and write the answer in simplest fraction form)


(e) (2 pts) If event A is “Getting a number greater than 3 in the first toss” and event B is “The sum of two tosses is at least 9”. Are event A and event B independent? Use statistical concept and mathematical expression to justify your answer.
I appreciate any help you can offer!
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi  

Assume that you toss a fair six-faced die two times

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)



(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 



(3,1) (3,2) (3,3) (3,4) (3,5) highlight%283%29,6 



(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 



(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 



(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)



a) 36 Outcomes

b) P(3 first) = 6(underlined)/36 = 1/6



-----------------

___1_2_3__4__5__6

1|_2_3_4__5__6__7

2|_3_4_5__6__7__8

3|_4_5_6__7__8__9

4|_5_6_7__8__9_10

5|_6_7_8__9_10_11

6|_7_8_9_10_11_12

c) P( Sum >=9) = 10/36  | Yes, good counting! P = 5/18

d) P(A|B) = P(A and B)/P(B)

P( Sum >=9) | 3 first) = %281%2F36%29++%2F%286%2F36%29 = 1/6

count them -  only one 3 first AND >=9 (highlighted)

e) P(A|B) = P(A and B)/P(B)

P( Sum >=9) |first > 3) 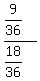%289%2F36%29%2F%2818%2F36%29 = 9/18 = 1/2  Count them

Conditional Probability:  Two events are not Independent 

Event: where Sum >=9, depends on the parameters put of the first draw