.
Jimmy and Dean were in a yacht race from Auckland to Suva, a distance of 1200km. Jimmy left port in Auckland two hours after Dean.
He sailed at an average speed which was 2km/h faster than Dean and finished in Suva exactly one day before him.
Given that the average speed is distance/time then find Dean's average speed during the yacht race.
~~~~~~~~~~~~~~~~~~~~~~~~
Solution 1. One quadratic equation.
Your governing equation is
= 
,
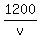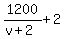where "v" is the Dean's speed, in 
.
Left side is the time Dean spent on his race.
Think what is the right side.
Solve the equation for "v". As a first step, multiply both sides by n*(v+2)
The rest is arithmetic.
Solution 2. Two equations in two unknowns.
The governing equations are
1200 = v*t, (1)
1200 = (v+2)*(t-2). (2)
These are the "D = RT" equations.
Again, "v" is the is the Dean's speed, in .
"t" is the time Dean spent on his race.
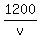To solve it, express t = from (1) and then substitute it in (2).
Then solve for "v".
For similar Travel and Distance problems see the lessons
- Travel and Distance problems
- Wind and Current problems
- More problems on upstream and downstream round trips
- Wind and Current problems solvable by quadratic equations
- Using fractions to solve Travel problems
- Unpowered raft floating downstream along a river
- Had a car move faster it would arrive quicker
- How far do you live from school?
- Selected Travel and Distance problems from the archive
- Selected problems from the archive on the boat floating Upstream and Downstream
- Selected problems from the archive on a plane flying with and against the wind
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referenced lessons are the part of this textbook (Travel and Distance problems of the section "Word problems").
