Question 1048633: Determine the value(s) of k such that the circle x^2+(y-6)^2 = 36 and the parabola x^2 = 4ky will intersect only at the origin.
Found 3 solutions by josgarithmetic, ikleyn, robertb:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! In trying to think of some algebraic steps to begin, putting in (0,0) for both equations makes for k=0. Note that the circle equations does not involve itself with k.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Determine the value(s) of k such that the circle x^2+(y-6)^2 = 36 and the parabola x^2 = 4ky will intersect only at the origin.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
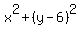 = 36, (1) = 36, (1)
 = 4ky (2)
The circle = 4ky (2)
The circle 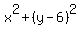 = =  has the center at (x,y) = (0,6) and has the radius of 6.
So, the circle has the y-axis x=0 as a diameter and as a symmetry line, passes through the origin and touches the x-axis.
Parabola has the center at (x,y) = (0,6) and has the radius of 6.
So, the circle has the y-axis x=0 as a diameter and as a symmetry line, passes through the origin and touches the x-axis.
Parabola  = = 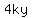 also passes through the origin; has the y-axis x=0 as its symmetry line, and touches the x-axis.
After these geometric considerations (that are useful but are not absolutely necessary) let solve the problem algebraically.
Based on (2), substitute 4ky instead of also passes through the origin; has the y-axis x=0 as its symmetry line, and touches the x-axis.
After these geometric considerations (that are useful but are not absolutely necessary) let solve the problem algebraically.
Based on (2), substitute 4ky instead of  into the equation (1). You will get into the equation (1). You will get
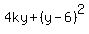 = 36.
So, in this way you excluded "x" from the system and got a single equation for "y". Let us simplify it: = 36.
So, in this way you excluded "x" from the system and got a single equation for "y". Let us simplify it:
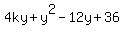 = 36, or = 36, or
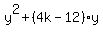 = 0. (1)
Now, the problem requires this equation (1) to have only one non-negative solution.
(One solution is evident/obvious. It is y = 0.)
It implies that (4k-12) MUST be non-positive: 4k-12 <= 0.
OTHERWISE y = = 0. (1)
Now, the problem requires this equation (1) to have only one non-negative solution.
(One solution is evident/obvious. It is y = 0.)
It implies that (4k-12) MUST be non-positive: 4k-12 <= 0.
OTHERWISE y = 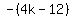 would be the other non-negative solution to (1).
So, the solution to the problem is this inequality 4k-12 <= 0, or, equivalently, k <= 3 (3 = would be the other non-negative solution to (1).
So, the solution to the problem is this inequality 4k-12 <= 0, or, equivalently, k <= 3 (3 =  )
Answer. k <= 3. )
Answer. k <= 3.
See an illustration below for k = 3, 2, and 4.

The circle 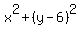 = =  (red + green) (red + green)
and three parabolas x^2 = 4ky for k=3 (blue), k=2, and k=4.

The circle 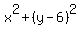 = =  (green) (green)
and three parabolas x^2 = 4ky for k=3 (blue), k=2, and k=4.
For solution of similar problems see the lesson
- Solving systems of algebraic equations of degree 2
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! From the system  and and  we fast-forward to the point where, after substitution and a little algebra, we get we fast-forward to the point where, after substitution and a little algebra, we get
 . .
Case 1.
We know beforehand that the two curves intersect at (0,0). To ensure that the above equation has at least one solution, let the discriminant

===>  ===> ===>  . .
Now when k = 3, the circle will "fit" snugly on the parabola at the origin, hence intersect only at that point.
We focus on the instance k > 3.
===>  ===> y = 0, -(4k-12). ===> y = 0, -(4k-12).
But  . If k > 3 are plugged into . If k > 3 are plugged into  , we will be solving for , we will be solving for  , a contradiction, hence not producing new solutions other than the origin. , a contradiction, hence not producing new solutions other than the origin.
Therefore, for k in [3,  ), the parabola ), the parabola  will intersect the circle only at the origin. will intersect the circle only at the origin.
Case 2. For k in ( , 0]: , 0]:
If k = 0,  becomes becomes  , or the vertical line x = 0, which is not a parabola, so k = 0 is excluded. , or the vertical line x = 0, which is not a parabola, so k = 0 is excluded.
For k < 0, the parabola opens downward (can accept only negative y values), hence it will automatically intersect the circle only at the origin.
Case 3. 0 < k < 3:
It can be shown that for 3/2 < k < 3, the parabola will intersect the circle at two points of equal level at the LOWER semicircular part.
For k = 3/2, the parabola intersects at the points (-6,6) and (6,6) (the diametrical points!).
For 0 < k < 3/2, the parabola will intersect the circle at two points of equal level at the UPPER semicircular part.
Therefore for Case 3, there are exactly 3 points of intersection, including the origin.
The final answer, therefore, is that k should be in ( ,0)∪[3, ,0)∪[3,  ), for the origin to be the ONLY intersection point. ), for the origin to be the ONLY intersection point.
|
|
|