SOLUTION: Solve the system and graph the curves: b) (y-2)^2 = 9(x+2) ;and 9x^2+4y^2+18x-16y = 0

(y-2)^2 = 9(x+2),               (1)
9x^2 + 4y^2 + 18x - 16y = 0.    (2)

Open parentheses in the first equation. Then the system is equivalent to

y^2 - 4y + 4 - 9(x+2) = 0,
9x^2 + 4y^2 + 18x - 16y = 0,   or

     -  9x + y^2  -  4y = 14,   (3)
9x^2 + 18x + 4y^2 - 16y =  0.   (4)

Multiply equation (3) by -4 (both sides), and then add to equation (3). You will get

9x^2 + 54x = -54,  or

x^2 + 6x + 6 = 0.

Apply the quadratic formula to find the roots. You will get

 =  =  = .


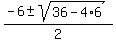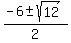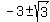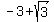For  = , you have from (1)

(y-2)^2 = 9*(x+2) = 9*(-1 + sqrt(3)), and  = .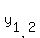 


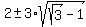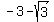For  = , you have from (1)

(y-2)^2 = 9*(x+2) = 9*(-1 - sqrt(3)), and the solution to (y-2) does not exist, since the right side 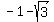 is negative.


So, there are two solutions (and, correspondingly, two intersection points)

 
     x = 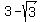  and   = ,   = . 


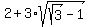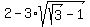To graph the curves, notice that

y - 2 = +/- 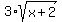,                  ( from (1), and )
9*(x+1)^2 - 9 + 4*(y-2)^2 - 16 = 0.     ( from (2) )   or


y       = ,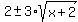
(y-2)^2 = .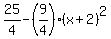


So the plot is