Question 1048375: To determine the height AB of a tree, Nancy places a mirror on the ground at E. From E, she walks backwards to a point D, where she is just about to see the top of the tree in the mirror. Given BE=18m,ED=2.4m, angle CED = angle AEB, and that her eyes are 1.6 m off the ground, find the height of the tree.
The answer is 12m, I don't get how!
Answer by ikleyn(52794)   (Show Source):
You can put this solution on YOUR website! .
To determine the height AB of a tree, Nancy places a mirror on the ground at E. From E, she walks backwards to a point D,
where she is just about to see the top of the tree in the mirror. Given BE=18m, ED=2.4m, angle CED = angle AEB,
and that her eyes are 1.6 m off the ground, find the height of the tree.
The answer is 12m, I don't get how!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Make a sketch, please.
The point B is on the ground, where the tree is standing.
The point A is the top of the tree.
The point D is on the ground, where Nancy is standing.
The point C is where Nancy's eyes are.
The triangles BAE and DCE are similar.
Why? They are right-angled triangles, and, in addition, you are given that
angle CED = angle AEB. (The last is the Reflection Law for a mirror).
Since the triangles are similar, their corresponding sides are proportional:
 =  .
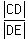Substitute the given data. You will get
 =  .
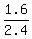Find the unknown value of |AB| from this proportion.
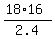|AB| =  = 12 m (coincides with your answer !)
Now you know why.
On triangles similarity, see the lessons
- Similar triangles
- Similarity tests for triangles
- Proofs of Similarity tests for triangles
- In a triangle a straight line parallel to its side cuts off a similar triangle
- Problems on similar triangles
- Similarity tests for right-angled triangles
- Problems on similarity for right-angled triangles
- Problems on similarity for right-angled and acute triangles
- One property of a median in a triangle
- One property of a trapezoid
- Miscellaneous problems on similar triangles
- Solved problems on similar triangles
in this site.
|
|
|
