SOLUTION: If 1/4= 1/A + 1/B where A and B are different whole numbers, find the value of A+B Can you please do this question also with 1/5 replacing 1/4 in the question?

Algebra ->  Expressions-with-variables -> SOLUTION: If 1/4= 1/A + 1/B where A and B are different whole numbers, find the value of A+B Can you please do this question also with 1/5 replacing 1/4 in the question?      Log On


   

Question 1048316: If 1/4= 1/A + 1/B where A and B are different whole numbers, find the value of A+B
Can you please do this question also with 1/5 replacing 1/4 in the question?
Answer by Edwin McCravy(20063) About Me  (Show Source):
You can put this solution on YOUR website!
1%2F4=+1%2FA+%2B+1%2FB

AB+=+4B+%2B+4A

AB+=+4%28B%2BA%29

Since AB is a multiple of 4, there are two possibilities;

Case 1. One of them, A or B, is odd and the 
other a multiple of 4. 

Case 2. Both A and B are even

-----------------------------------

Case 1: Say A is a multiple of 4 and B is odd

A = 4p,  B = 2q-1, for some positive integers p and q

%284p%29%282q-1%29=4%282q-1%2B4p%29

p%282q-1%29=2q-1%2B4p

2pq-p=2q-1%2B4p
2pq-5p=2q-1
p%282q-5%29=2q-1
p=%282q-1%29%2F%282q-5%29
p=%282q-5%2B5-1%29%2F%282q-5%29
p=%282q-5%2B4%29%2F%282q-5%29
p=%282q-5%29%2F%282q%2B5%29%2B4%2F%282q-5%29
p=1%2B4%2F%282q-5%29

So 4 must be divisible by 2q-5

2q-5 = 1,2, or 4
  2q = 6,7, or 9

Since 2q is even, it can only be 6
  2q = 6
   q = 3
p=1%2B4%2F%282q-5%29
p=1%2B4%2F%282%283%29-5%29
p=1%2B4%2F%286-5%29
p=1%2B4%2F1
p=1%2B4
p=5

A = 4p,    B = 2q-1
A = 4(5)   B = 2(3)-1
A = 20     B = 6-1
A = 20     B = 5

Checking 1%2FA%2B1%2FB=1%2F20%2B1%2F5=1%2F20%2B4%2F20=5%2F20=1%2F4

One solution is {A,B} = {20,5}

-------------------------------

Case 2:  Both A and B are even

A = 2p,  B = 2q, for some positive integers p and q

AB+=+4B+%2B+4A

%282p%29%282q%29=4%282q%29%2B4%282p%29

4pq=8q%2B8p

pq=2q%2B2p

pq-2p=2q
p%28q-2%29=2q
p=2q%2F%28q-2%29
p=%282q-4%2B4%29%2F%28q-2%29
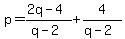
p=%282q-4%29%2F%28q-2%29%2B4%2F%28q-2%29
p=%282%28q-2%29%29%2F%28q-2%29%2B4%2F%28q-2%29
p=2%2B4%2F%28q-2%29

So 4 must be divisible by q-2

q-2 =  1; 2; 4 
  q =  3; 4; 6 

Substitute in p=2%2B4%2F%28q-2%29

  p =  6; 4; 3
  A = 12; 8; 6 
  B =  6; 8;12

A and B are different, so that rules out the 8's,
so one is 6 and the other 12.

Checking: 1%2F6%2B1%2F12=2%2F12%2B1%2F12=3%2F12=1%2F4

So there are two solutions:

{A,B} = {20,5}

and

{A,B} = {12,6}

Edwin