Question 1047933: Is this statement true or false and why?
If you are given the 2 functions of 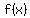 and and 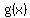 you can calculate(f ○ g) you can calculate(f ○ g)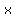 only if the range of only if the range of 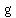 is a subset of the domain of is a subset of the domain of 
Found 2 solutions by robertb, ikleyn:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! To this "tutor" "ikleyn":
You mentioned--
"2. In order for calculate (fog)(x) for ALL [caps mine] x from the domain of the function g, the range of g ("the image of g") must lie in the domain of the function f."
MY RESPONSE---NO, you are WRONG. In general the entire domain of g(x) doesn't have to be sent by g as a subset of the domain of f(x) in order for (f o g)(x) to be CALCULATED.
The basic question is: For x in the domain of g, will g(x) be in the domain of f? THIS MAY OR MAY NOT BE.
For example, take  , which takes the closed interval [0,2] onto the closed interval [0,1]; and let , which takes the closed interval [0,2] onto the closed interval [0,1]; and let  . .
f takes [1/2,  ) onto [0, ) onto [0,  ). ).
Obviously, the range of g, [0,1], is NOT a subset of the domain of f, [1/2,  ), BUT their intersection [1/2,1], is apparently NON-EMPTY. The pullback of this interval, the interval [1, ), BUT their intersection [1/2,1], is apparently NON-EMPTY. The pullback of this interval, the interval [1, 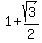 ], obviously a subset of [0,2], consists of all x in the domain of g where we can make meaningful calculations for (f o g)(x). ], obviously a subset of [0,2], consists of all x in the domain of g where we can make meaningful calculations for (f o g)(x).
Furthermore, nowhere in the statement of problem of the asker does he/she say that the calculation of (f o g)(x) has to be for ALL x in the domain of g, because there are intrinsic qualities in the definition of functions that in general will limit the use of the entire domain of g, especially when function composition is involved.
And NO, his original statement is NOT ambiguous...
------------------------------------------------------------------------------
------------------------------------------------------------------------------
This is FALSE.
It is only required that the intersection of the range of g(x) and the domain of f(x) is NON-EMPTY.
The pullback of this intersection (which is a subset of the domain of g(x)), has to be NON-EMPTY as well,
for any calculation of (f o g)(x) to occur.
Answer by ikleyn(52803)   (Show Source): (Show Source):
|
|
|