Question 1047753: find three consecutive odd integers such that the sum of the least integer and the middle integer 19 more than the great integer
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
find three consecutive odd integers such that the sum of the least integer and the middle integer 19 more than the great integer
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let A = 2n+1 be the first (the least) of the three consecutive odd integers;
B = 2n+3 be the second of the three consecutive odd integers; and
C = 2n+5 be the third.
The condition requires
A + B = C + 19, or
(2n+1) + (2n+3) = (2n+5) + 19.
Simplify:
2n + 1 + 2n + 3 = 2n + 5 + 19,
2n + 4 = 24,
2n = 24 - 4 = 20,
n = 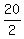 = 10.
So, your numbers are A = 2n+1 = 2*10+1 = 21; B = 21+2 = 23; and C = 23+2 = 25.
Check. A + B = 21 + 23 = 44.
44 - 19 = 25. Correct !
Answer. The numbers are 21, 23 and 25.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
find three consecutive odd integers such that the sum of the least integer and the middle integer 19 more than the great integer
Let the smallest integer be S
Then middle = S + 2, and largest = S + 4
We then get: S + S + 2 = S + 4 + 19
2S + 2 = S + 23
2S - S = 23 - 2
S, or smallest integer = 
|
|
|
