.
The area of a rectangle is 30 and its diagonal is sqrt(61) Find its dimensions and perimeter.
~~~~~~~~~~~~~~~~~~~~~~~
Answer. The rectangle is 6x5 and its perimeter is 6 + 5 + 6 + 5 = 22 units.
xy = 30, (1)
= 61. (2)
Multiply eq.(1) by 2 and then add to eq.(2) (both sides). You will get
= 61 + 60, or
= 121.
Then x + y = 
= 11.
Express x = 11-y from the last equation. Then substitute this expression into (1). You will get
(11-y)*y = 30, or
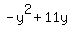= 30, or
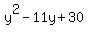= 0.
Factor left side:
(y-5)*(y-6) = 0.
The roots are y = 5 and/or y = 6.
Solved.
