SOLUTION: There is a question on the practice Compass test I don't understand. It is; For all nonzero r, t, and z values, 16(r^3)t(z^5)/(-4)r(t^3)(z^2) = ? I have seen how this problem

Algebra ->  Exponents -> SOLUTION: There is a question on the practice Compass test I don't understand. It is; For all nonzero r, t, and z values, 16(r^3)t(z^5)/(-4)r(t^3)(z^2) = ? I have seen how this problem      Log On


   

Question 1047425: There is a question on the practice Compass test I don't understand. It is;
For all nonzero r, t, and z values, 16(r^3)t(z^5)/(-4)r(t^3)(z^2) = ?
I have seen how this problem is solved, but I don't know what the process is called or where to find more problems like this one so I can try the process of solving it again to be sure I understand it.
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
For all nonzero r, t, and z values,
Simplify:(I say SIMPLIFY because you don't know the values of r, t, or z, so you cannot EVALUATE or SOLVE).
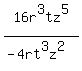16r%5E3tz%5E5%2F%28-4rt%5E3z%5E2%29 To simplify, you want to cancel like-factors in the numerator and the denominator. If you are not sure how to do this, you can rewrite the expression showing the factors:
Cancel the indicated like-factors to leave you with:
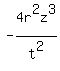
-4r%5E2z%5E3%2Ft%5E2
here we see that t is in denominator, so t cannot be equal to zero,
so, solution set for+t is:
{ t is element of R: t%3C%3E0 }

and, solution set for r and is: all real numbers
{ r is element of R }
{ z is element of R }