Question 1047332: Please find the minimum and maximum values of the expression 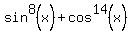 . .
Found 3 solutions by josmiceli, robertb, ikleyn:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Well, I am sending this commentary to "ikleyn"--
Of course, it will be "SLIGHTLY SHIFTED".
One MISTAKE you made was that you plotted  as if x was the independent variable in the function, and over the SAME COORDINATE SYSTEM! It was NOT. as if x was the independent variable in the function, and over the SAME COORDINATE SYSTEM! It was NOT.
Remember, I let  . .
So naturally, the lowest points of the two graphs will NOT jive. BUT, what is guaranteed is that they will have the SAME LOWEST level.
Another MISTAKE you made was that, z is a composite function, and as such, its domain, as a function of w, is only  . Meaning, your green-colored graph is WRONG. . Meaning, your green-colored graph is WRONG.
The range of z is [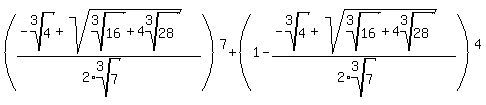 ,1], or[0.05310578625,1] (approximately). ,1], or[0.05310578625,1] (approximately).
In fact, I can even predict/estimate the amount of "shift" that you're talking about:
 . .
Naughty, naughty, not so smarty....
----------------------------------------------------------------------------------------------------------------
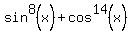
= 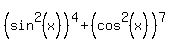
= 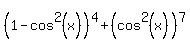
Now let  . ===> . ===>  , and , and
===>  . .
Let  . .
===>  . Letting this equal to zero, we get . Letting this equal to zero, we get
 . .
===>  , after taking cube root of both sides. , after taking cube root of both sides.
===>  . .
===> 
=  , since , since  . .
≈ 0.5860760201.
Now to the left of 0.5860760201, z' < 0, so z is decreasing on [0, 0.5860760201).
To the right of 0.5860760201, z' > 0, so z is increasing on (0.5860760201,1].
Hence there is a local minimum at w = 0.5860760201.
We only need to check the other critical points where the derivative doesn't exist, namely at w = 0 and w = 1,
to determine the other possible extrema.
At w = 0, z = 1.
At w = 1, z = 1.
Therefore the maximum of 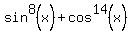 is is  , while the minimum is , while the minimum is
 , approximately. , approximately.
Answer by ikleyn(52903)   (Show Source): (Show Source):
|
|
|