Question 1047218: Please help on this probability question. I got 1/16 as an answer by multiplying (1/2)*(1/2)*(1/2)*(1/2) = 1/16 I am not sure if I am right.
A couple decides to have 4 children. If they succeed in having4 children and each child is equally likely to be a boy or a girl, what is the probability that they will have exactly 2 girls and 2 boys?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
is the probability that they will have
girl, girl, girl, girl, in that order.
It is also the probability of
boy, boy, boy, boy, in that order,
and it is the probability of any sequence of 4 children,
such as
boy, boy, girl, girl, or
girl, girl, boy, boy, or
boy, girl, boy, girl, or
girl, boy, girl, boy, or
boy, girl, girl, boy, or
girl, boy, boy,girl.
So out of the  sequences possible sequences possible
there are  sequences that would give them exactly 2 girls and 2 boys. sequences that would give them exactly 2 girls and 2 boys.
The probability of that is  . .
When you are faced with problems of that sort,
think of 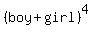 or or 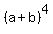 . .
In the painful  multiplication, multiplication,
you would end with  products, products,
including 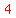 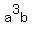 product terms, product terms,  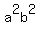 , and , and 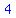 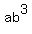 , ,
but then you "collect like terms" to get
 . .
The term 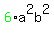 tells you that there were tells you that there were 
outcomes where 2 a's and 2 b's happened, in various orders.
The probability of that happening is 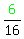 . .
|
|
|