|
Question 1047141: Please help! I do not seem to understand the question. May be the question is wrongly put on exam.
When a positive integer n is divided by 5, the remainder is 1. When n is divided 7, the remainder is 3. What is the smallest positive integer k such that is a multiple of 35?
Found 3 solutions by Edwin McCravy, MathLover1, AnlytcPhil:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
Something's wrong. The first two sentences talk only about n,
never mentioning k. Then the last sentence asks about k, and
doesn't even mention n. I'll try to make something of it anyway.
I think the problem should have been: When a positive integer n is divided by 5, the
remainder is 1. When n is divided 7, the remainder
is 3. What is the smallest possible positive integer n? If when n is divided by 5, the remainder is 1,
then it is 1 more than a multiple of 5. So
there is a positive integer p such that n = 5p+1
If when n is divided by 7, the remainder is 3,
then it is 3 more than a multiple of 7. So
there is a positive integer q such that n = 7q+3
So n = 5p+1 = 7q+3
5p = 7q+2
5p = 5q+2q+2
p = q + (2/5)q + 2/5
p-q = (2/5)q + 2/5
The left side is an integer so the right side is too.
Let that integer be A
p-q = (2/5)q + 2/5 = A
(2/5)q + 2/5 = A
2q + 2 = 5A
2q + 2 = 4A + A
q + 1 = 2A + A/2
q + 1 - 2A = A/2
The left side is an integer so the right side is too.
Let that integer be B
q + 1 - 2A = A/2 = B
A/2 = B
A = 2B
q + 1 - 2A = B
q + 1 - 2(2B) = B
q + 1 - 4B = B
q + 1 = 5B
q = 5B-1
p-q = A
p - (5B-1) = 2B
p - 5B + 1 = 2B
p = 7B-1
n = 5p+1 = 7q+3
n = 5(7B-1)+1 = 7(5B-1)+3
n = 35B-5+1 = 35B-7+3
n = 35B-4 = 35B-4
4 is less than either 5 or 7, so let C = B-1, B = C+1
n = 35(C+1)-4
n = 35C+35-4
n = 35C+31
Since 35C divided by 5 or 7 there is 0 remainder. Therefore,
1. When we divide n by 5 we get the same remainder as when
we divide 31 by 5, which gives a remainder of 1.
2. When we divide n by 7 we get the same remainder as when
we divide 31 by 7, which gives a remainder of 3.
So the smallest integer that when divided by 5, the remainder
is 1, and when divided by 7, the remainder is 3 is when C=0
or n = 31.
That's what I think was the intended answer.
It would be impossible for n ever to be a multiple of 35, so
the misprint (typo) could not have been that k was supposed
to be n.
So the last sentence was probably from another problem, and
somehow it got placed on the wrong problem.
Edwin
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website!
The number  is such that it has to satisfy these two series
a.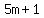 
b.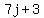 
To solve these types first take the  of the multiples  and {{7}}} here =  .
So the resulting series will be:
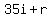
Now we find  . To do this set  and try to find the first term in the series  and  that is  .
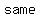series a.  , , , , ,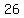
series b.  , , ,,
So it matches at . So 
Therefore the resulting series is :
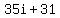
So the smallest number which needs to be added to this is  to make it divisible by .
Therefore, answer is 
Answer by AnlytcPhil(1806)  (Show Source):
You can put this solution on YOUR website!
Her interpretation can't be right. The question asks: What is the smallest positive integer k such that is a multiple of 35?She has the answer as k = 4. But 4 is not a multiple of 35.
Edwin
|
|
|
| |
