Question 1047115: The lines y = 3x - 25 and y = -3/4x + 17 intersect at point P. How far is P from the origin?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  .......eq.1 .......eq.1
 .......eq.2 .......eq.2
-----------------------------------since left sides equal, we have
 ......solve for ......solve for 






or approximately

find  : :
 .......eq.1 .......eq.1



or approximately

so, the lines intersect at point P (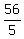 , , ) )
to find out how far is P from the origin ( , , ), use distance formula: ), use distance formula:
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (0, 0), we can say (x1, y1) = (0, 0)
So  , , 
Since the second point is (11.2, 8.6), we can also say (x2, y2) = (11.2, 8.6)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (0, 0) and (11.2, 8.6)

 Plug in Plug in  , ,  , ,  , and , and 




==========================================================
Answer:
The distance between the two points (0, 0) and (11.2, 8.6) is exactly 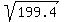 units units
The approximate distance between the two points is about 14.1209064864831 units
So again,
Exact Distance: 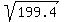 units units
Approximate Distance: 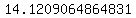 units units
|
|
|
|