SOLUTION: Determine the fourth roots of -16

Algebra ->  Geometry-proofs -> SOLUTION: Determine the fourth roots of -16      Log On


   

Question 1046939: Determine the fourth roots of -16
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
Determine the fourth roots of -16
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

In the complex plane, -16 = 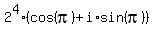2%5E4%2A%28cos%28pi%29+%2B+i%2Asin%28pi%29%29.

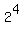The modulus of -16 is 2%5E4, the argument is pi.

Therefore, according to the general theory, the fourth roots of -16 are four complex numbers


   1)  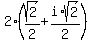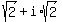2%2A%28cos%28pi%2F4%29+%2B+i%2Asin%28pi%2F4%29%29 =                                       2%2A%28sqrt%282%29%2F2%2Bi%2Asqrt%282%29%2F2%29        = sqrt%282%29%2Bi%2Asqrt%282%29;

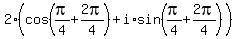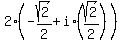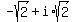   2)  2%2A%28cos%28pi%2F4+%2B+2pi%2F4%29+%2B+i%2Asin%28pi%2F4%2B2pi%2F4%29%29 = 2%2A%28cos%283pi%2F4%29%2Bi%2Asin%283pi%2F4%29%29 = 2%2A%28-sqrt%282%29%2F2+%2B+i%2A%28sqrt%282%29%2F2%29%29   = -sqrt%282%29+%2B+i%2Asqrt%282%29;

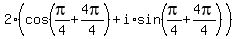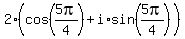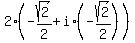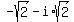   3)  2%2A%28cos%28pi%2F4+%2B+4pi%2F4%29+%2B+i%2Asin%28pi%2F4%2B4pi%2F4%29%29 = 2%2A%28cos%285pi%2F4%29%2Bi%2Asin%285pi%2F4%29%29 = 2%2A%28-sqrt%282%29%2F2+%2B+i%2A%28-sqrt%282%29%2F2%29%29%29 = -sqrt%282%29+-+i%2Asqrt%282%29;

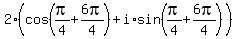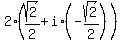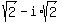   4)  2%2A%28cos%28pi%2F4+%2B+6pi%2F4%29+%2B+i%2Asin%28pi%2F4%2B6pi%2F4%29%29 = 2%2A%28cos%287pi%2F4%29%2Bi%2Asin%287pi%2F4%29%29 = 2%2A%28sqrt%282%29%2F2+%2B+i%2A%28-sqrt%282%29%2F2%29%29%29  = sqrt%282%29+-+i%2Asqrt%282%29.


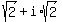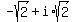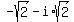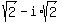Answer.  The four values of fourth root of -16 are  sqrt%282%29%2Bi%2Asqrt%282%29,  -sqrt%282%29+%2B+i%2Asqrt%282%29,  -sqrt%282%29+-+i%2Asqrt%282%29  and   sqrt%282%29+-+i%2Asqrt%282%29.

For this "general theory" see the lesson
    - How to take a root of a complex number
in this site.

There is a bunch of my lessons on complex numbers
    - Complex numbers and arithmetical operations on them
    - Complex plane
    - Addition and subtraction of complex numbers in complex plane
    - Multiplication and division of complex numbers in complex plane
    - Raising a complex number to an integer power
    - How to take a root of a complex number
    - Solution of the quadratic equation with real coefficients on complex domain
    - How to take a square root of a complex number
    - Solution of the quadratic equation with complex coefficients on complex domain
in this site.