Question 1046879: A boat travels 80 km downstream in 2.5 hours. It travels 50 km upstream in the same length of time. what is the speed of the boat in still water and of the current?
Thank you
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is too common a type of question so I will begin to answer purely in symbols. Your boat is able to move faster going downstream, but if in still water, assigning the rate or speed r.
SPEED TIME DISTANCE
DOWNSTR r+c t D
UPSTRM r-c t d

 -------two equations in two unknown variables; the others are given and constant knowns. -------two equations in two unknown variables; the others are given and constant knowns.
Solve for c and r.



-





 -------formula for the still-water speed -------formula for the still-water speed
Note, I used substitution, but Elimination might be a possible choice to use. Elimination being used in finding c, next.
 just subtraction corresponding members of the two equations of the system just subtraction corresponding members of the two equations of the system
 , which immediately seems more efficient a method... , which immediately seems more efficient a method...
 ------river current speed ------river current speed
---
AFTER-THOUGHT
A better way, nearly the same as I showed, would be, fill-in the table with the ACTUAL values first, and of course the UNKNOWN variables too, AND THEN make the generalizations for ALL THE GIVEN VALUES. Now make a new table, but use only variables for everything.
NOW you can more comfortably write your system of equations, and keep in mind which variables are the unknowns. Solve this system purely in variables. You will have formulas for each unknown variable from that.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A boat travels 80 km downstream in 2.5 hours. It travels 50 km upstream in the same length of time.
what is the speed of the boat in still water and of the current?
~~~~~~~~~~~~~~~~~~~~~~~~~~
For the trip downstream, your first equation is
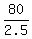 = u + v, or
32 = u + v. (1)
The term in the left side is the speed of the boat (relative to the bank of the river) on the trip downstream with the river current.
Here u is the boat speed in still water and v is the current speed.
For the upstream trip, your second equation is = u + v, or
32 = u + v. (1)
The term in the left side is the speed of the boat (relative to the bank of the river) on the trip downstream with the river current.
Here u is the boat speed in still water and v is the current speed.
For the upstream trip, your second equation is
 = u - v, or
20 = u - v. (2)
The term in the left side is the speed of the boat (relative to the bank of the river) on the trip upstream against the river current.
Again, here u is the boat speed in the still water and v is the current speed.
Rewrite the equations (1) and (2) in this way:
u + v = 32, (3)
u - v = 20. (4)
To solve them, add equations (3) and (4) (both sides). You ill get
2u = 32 + 20, or 2u = 52. Hence, u = = u - v, or
20 = u - v. (2)
The term in the left side is the speed of the boat (relative to the bank of the river) on the trip upstream against the river current.
Again, here u is the boat speed in the still water and v is the current speed.
Rewrite the equations (1) and (2) in this way:
u + v = 32, (3)
u - v = 20. (4)
To solve them, add equations (3) and (4) (both sides). You ill get
2u = 32 + 20, or 2u = 52. Hence, u = 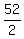 = 26.
You just found the speed of the boat in still water. It is 26 mph.
Now from (3) v = 32 - u = 32 - 26 = 6.
Thus the current rate is 6 mph.
Answer. The speed of the boat in still water is 32 mph. The current rate is 6 mph. = 26.
You just found the speed of the boat in still water. It is 26 mph.
Now from (3) v = 32 - u = 32 - 26 = 6.
Thus the current rate is 6 mph.
Answer. The speed of the boat in still water is 32 mph. The current rate is 6 mph.
For many other solved problems on upstream and downstream trips see the lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Selected problems from the archive on the boat floating Upstream and Downstream
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
|
|
|