Question 1046749: Having Problem with this question.
Prove that the sets of irrational numbers Q^c, the set of rational numbers Q and the set of integers Z are not open
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! For numbers in the real number line...
---Any subset is called an OPEN set if, for any element of the subset,
an open interval centered at the element can be found that is entirely
inside the subset.
1) For the set of irrationals 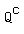 , surrounding any irrational number by an open interval, no matter how small, will contain elements outside of it (i.e., rationals). Therefore , surrounding any irrational number by an open interval, no matter how small, will contain elements outside of it (i.e., rationals). Therefore 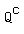 is not open. is not open.
2) The same thing can be said with Q, the set of all rationals. Surrounding any rational number by an open interval, no matter how small, will contain elements outside of it (i.e., irrationals). Therefore Q is not open.
3) The set of all integers Z is likewise not open, since you can choose to surround any integer by an open interval small enough such that it will
not contain any integer.
|
|
|