Question 1046557: For any triangle ABC, we have cosA + cosB + cosC =1+4SinA/2SinB/2SinC/2
and SinA/2 + SinB/2 + SinC/2=< 1/8
Use the above facts to prove that for any triangle 1,CosA+CosB+CosC=<3/2
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! I will prove an even better upper bound!

===>  , ,
by directly substituting the given inequality...
Now  ===> ===>  , which means A/2, B/2, and C/2 are acute angles, hence all sines and cosines for these angles are positive. , which means A/2, B/2, and C/2 are acute angles, hence all sines and cosines for these angles are positive.
Now let  , and , and  . .
===>  . .
The restrictions are 0 < x,y < 1.
===>  ===> ===>  , and , and 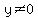 . .
===>  . .
Similarly, after taking 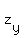 and solving for and solving for  with with  , we get , we get
 . .
===> the critical point is at (1/24, 1/24).
Since there is only one critical point and the domain of definition is the open square (0,1)x(0,1), there is an absolute extremum (maximum)
at the point (1/24, 1/24).
The maximum value of  is thus is thus  , ,
which is around 1.000289.
===>  . .
|
|
|