Question 1046549: Katie has a collection of nickels, dimes and quarters with a total value of
$6.70. There are 3 more dimes than nickels and 8
more quarters than nickels, how many of each coin does she have?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Multiply the money count equation by 20.

Find two convenient substitutions to do, and first solve for n using the money count equation.
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Katie has a collection of nickels, dimes and quarters with a total value of
$6.70. There are 3 more dimes than nickels and 8
more quarters than nickels, how many of each coin does she have?
Let number of nickels, dimes, and quarters, be N, D, and Q, respectively
Then, .05N + .1D + .25Q = 6.7 ------- eq (i)
Also, D = N + 3 ------ eq (ii)
And, Q = N + 8 ------- eq (iii)
.05N + .1(N + 3) + .25(N + 8) = 6.7 ------- Substituting N + 3 for D, and N + 8 for Q in eq (i)
.05N + .1N + .3 + .25N + 2 = 6.7
.4N + 2.3 = 6.7
.4N = 6.7 - 2.3
.4N = 4.4
N, or number of nickels = 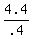 , or , or 
Number of dimes: 11 + 3, or 
Number of quarters: 11 + 8, or 
|
|
|