SOLUTION: A woman paddling a canoe downstream with the river current travels 20 miles in 2 hours. On the return trip, she paddles the same distance upstream against the river current in 5 ho

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: A woman paddling a canoe downstream with the river current travels 20 miles in 2 hours. On the return trip, she paddles the same distance upstream against the river current in 5 ho      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1046453: A woman paddling a canoe downstream with the river current travels 20 miles in 2 hours. On the return trip, she paddles the same distance upstream against the river current in 5 hours. Write and solve a system of two linear equations to determine the rate of the boat in calm water and the rate of the current, both in miles per hour.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39615) About Me  (Show Source):
You can put this solution on YOUR website!
This type or form of travel rates problems is so frequent that a general solution is a good idea.

Let x and y be time quantities and y%3Ex.
Let r and c be canoe rate in still water and c be rate of river current. 
                      RATE         TIME       DISTANCE
WITH CURRENT          r+c          x          d
AGAINST CURRENT       r-c          y          d


KNOWN VARIABLES
x, y, d
UNKNOWN VARIABLES
r, c

system%28x%28r%2Bc%29=d%2Cy%28r-c%29=d%29
Solve this system of equations for r and for c.

r%2Bc=d%2Fx
c=d%2Fx-r
-
y%28r-c%29=d
y%28r-%28d%2Fx-r%29%29=d
y%28r-d%2Fx%2Br%29=d
y%282r-d%2Fx%29=d
2r-d%2Fx=d%2Fy
2r=d%2Fy%2Bd%2Fx
r=%28d%2Fy%2Bd%2Fx%29%2F2
r=%28d%2F2%29%281%2Fy%2B1%2Fx%29
r=%28d%2F2%29%28x%2By%29%2F%28xy%29
highlight%28r=%28d%28x%2By%29%29%2F%282xy%29%29----------Or what ever form/format is most convenient


Use whatever method you want to solve for c. You can use the found r and other given data to directly evaluate c now, or use algebra skills to find a formula for c before evaluating.

Answer by ikleyn(52772) About Me  (Show Source):
You can put this solution on YOUR website!
.
A woman paddling a canoe downstream with the river current travels 20 miles in 2 hours.
On the return trip, she paddles the same distance upstream against the river current in 5 hours.
Write and solve a system of two linear equations to determine the rate of the boat in calm water and the rate of the current,
both in miles per hour.
~~~~~~~~~~~~~~~~~~~~~~~~~~ 

Your first equation is 

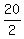20%2F2 = u + v,  or 

10 = u + v.   (1)

The term in the left side is the speed of the canoe (relative to the bank of the river) on the trip downstream with the river current.
Here u is the canoe speed in the still water and v is the current speed.


Your second equation is 

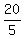20%2F5 = u - v,  or 

4 = u - v.   (2)

The term in the left side is the speed of the canoe (relative to the bank of the river) on the trip upstream against the river current.
Again, here u is the canoe speed in the still water and v is the current speed.


Rewrite the equations (1) and (2) in this way:

u + v = 10,   (3)
u - v =  4.   (4)

To solve them, add equations (3) and (4)  (both sides). You ill get

2u = 10 + 4,  or  2u = 14.  Hence,  u = 14%2F2 = 7.

You just found the speed of the canoe in still water. It is 7 mph.

Now from (3)  v = 10 - u = 10 - 7 = 3.

Thus the current rate is 3 mph.

Answer.  The speed of the canoe in still water is 7 mph.  The current rate is 3 mph.

For many other solved problems on upstream and downstream trips see the lessons
    - Wind and Current problems
    - More problems on upstream and downstream round trips
    - Selected problems from the archive on the boat floating Upstream and Downstream

Read them attentively and learn how to solve this type of problems once and for all.

Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.


Please ignore everything that the other tutor, "josgarithmetic", wrote in his post.
He neither knows how to solve it nor how to explain.