SOLUTION: How many different permutations can be formed using all the letters in the word MASSACHUSETTS?

The word MASSACHUSETTS contains 13 letters, of them "S" is repeating 4 times, "A" is repeating 2 times, "T" is repeating twice. 
The remaining letters are unique.


13 symbols create 13! permutations.

Of them, the number of distinguishable permutations is  =  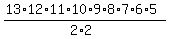= 13*12*11*10*9*2*7*6*5 = 64864800.

We divide 13! by k! for each symbol in the word repeating k times.