Question 1046376: At a cruising speed,Marie's small family plane can fly at 100 km/h. On a recent vacation trip, it took 3 h to fly with the wind to a resort and 7 h to fly back against the wind. What was the rate of the wind? How far away was the resort?
Please help me.
I'm not understanding uniform motion problems.
Found 3 solutions by solver91311, josgarithmetic, ikleyn:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
At a cruising speed,Marie's small family plane can fly at 100 km/h. On a recent vacation trip, it took 3 h to fly
with the wind to a resort and 7 h to fly back against the wind. What was the rate of the wind? How far away was the resort?
Please help me.
I'm not understanding uniform motion problems.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The plane can fly at 100 km/h in still air (with no wind).
For the given problem, let "v" be the wind speed and D be the distance.
When the plane flies with the wind, its speed relative to the ground is 100+v km/h.
Therefore, your first equation is
 = 100 + v. (1)
As a reminder, when you divide the distance by the time, you get the speed.
It is what is written in the equation (1).
When the plane flies against the wind, its speed relative to the ground is 100-v km/h.
Therefore, your second equation is = 100 + v. (1)
As a reminder, when you divide the distance by the time, you get the speed.
It is what is written in the equation (1).
When the plane flies against the wind, its speed relative to the ground is 100-v km/h.
Therefore, your second equation is
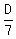 = 100 - v. (2)
Again, when you divide the distance by the time, you get the speed.
It is what is written in the equation (2).
Now all your problem is presented in equations (1) and (2). It is the system of two equations in two unknowns, D and v.
To solve it, let us first find D, the distance. For it, add the equations (1) and (2) (both sides). You will get a single equation for D: = 100 - v. (2)
Again, when you divide the distance by the time, you get the speed.
It is what is written in the equation (2).
Now all your problem is presented in equations (1) and (2). It is the system of two equations in two unknowns, D and v.
To solve it, let us first find D, the distance. For it, add the equations (1) and (2) (both sides). You will get a single equation for D:
 = 200, or (multiply both sides by 3*7)
7D + 3D = 200*3*7, or
10D = 4200, which gives you
D = = 200, or (multiply both sides by 3*7)
7D + 3D = 200*3*7, or
10D = 4200, which gives you
D = 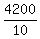 = 420 km.
So, you just found the distance. It is D = 420 km.
Now you can easily find the speed "v", which is under the question. From (1), you have
v = = 420 km.
So, you just found the distance. It is D = 420 km.
Now you can easily find the speed "v", which is under the question. From (1), you have
v =  = =  = 140 - 100 = 40 km/h.
The wind speed is 40 km/h.
Check. = 140 - 100 = 40 km/h.
The wind speed is 40 km/h.
Check.  = =  = 3 hours. = 3 hours.
 = = 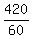 = 7 hours.
Answer. The speed of wind is 40 mph. = 7 hours.
Answer. The speed of wind is 40 mph.
For many other solved Travel and Distance problems see the lessons
- Travel and Distance problems
- Wind and Current problems
- More problems on upstream and downstream round trips
- Wind and Current problems solvable by quadratic equations
- Unpowered raft floating downstream along a river
- Selected Travel and Distance problems from the archive
- Selected problems from the archive on the boat floating Upstream and Downstream
- Selected problems from the archive on a plane flying with and against the wind
in this site.
|
|
|