Question 1046168: Hello, I'm new to these kind of questions so I have no idea where to start... The question is:
Tom bought a notebook with 100 sheets and numbered its pages consecutively from 1 to 200. Jerry pulled out 43 sheets and added up all 86 page numbers written on both sides of each of the sheets. Can the sum be equal to 2016?
Found 2 solutions by robertb, KMST:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, you must realize that, for ANY sheet of the notebook,
the front sheet will always be numbered ODD (and so the back page will always
be numbered even.)
Thus, the number pages of the sheets will form a sequence that looks like this:
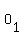 , , 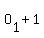 , , 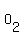 , , 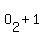 , , 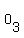 , , 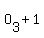 ,..., ,..., 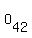 , , 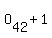 , , 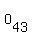 , , 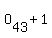 , ,
where  denotes the odd number paging of the front page of the kth sheet. denotes the odd number paging of the front page of the kth sheet.
Suppose we sum all of these pagings. The sum would be
 . .
Letting this equal 2016, we get
 . .
===>  . .
Contradiction.
Therefore the sum CANNOT be 2016.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Each sheet has two sides, with two consecutive page numbers:
1 and 2, on the first sheet, 3 and 4, on the second sheet, and so on.
The numbers on the  sheet were sheet were
 on the first side, and on the first side, and
 on the flip/back side. on the flip/back side.
Adding both of those numbers, you get  . .
Let's say the 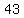 sheets Jerry pulled out were sheets number sheets Jerry pulled out were sheets number
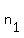 , , 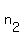 , ,  , ...., and , ...., and 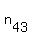
The sum of page numbers on those sheets is
 . .
The expression 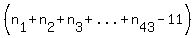 is definitely a positive integer, is definitely a positive integer,
so 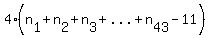 is definitely a multiple of is definitely a multiple of  , ,
and the sum,
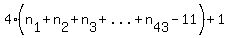 , ,
could not be a multiple of  . .
It could be
 , or , or
 , ,
but it could never be  . .
(It could not be 2014 or 2015, either).
|
|
|