Question 1045977: How many liters of an antifreeze that is 18% alcohol must be mixed with an antifreeze that is 10% alcohol to produce an antifreeze that is 15% alcohol
Found 2 solutions by addingup, ikleyn:
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! So, you're saying it doesn't matter how much antifreeze in total? If that's the case I can only give you a ratio that you can apply to 5 liters, or 15, or 150.
:
Personally, I think you're missing a key piece of information. I think your question should be: How many liters of each antifreeze solution should be combined to create 10 liters (or whatever liters) of antifreeze solution that is 15% alcohol?
:
Go check it out and re-upload the problem.
:
John
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many liters of an antifreeze that is 18% alcohol must be mixed with an antifreeze that is 10% alcohol to produce an antifreeze that is 15% alcohol
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "x" be a volume of the 18% antifreeze and "y" be a volume of the 18% antifreeze to mix.
Then the total volume is x+y;
The volume of the pure antifreeze in x liters of the 18% antifreeze is 0.18*x;
The volume of the pure antifreeze in y liters of the 10% antifreeze is 0.10*y;
The volume of the pure antifreeze in the mixture is 0.18x + 0.10y.
The condition on the concentration of the mixture says and requires
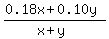 = 0.15, or
0.18x + 0.1y = 0.15*(x+y), or
0.18x - 0.15x = 0.15y - 0.1y, or
0.3x = 0.5y,
Then y = = 0.15, or
0.18x + 0.1y = 0.15*(x+y), or
0.18x - 0.15x = 0.15y - 0.1y, or
0.3x = 0.5y,
Then y = 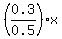 = = 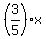 , or , or  = =  .
In other words, the ratio of the volume of the 10% antifreeze to the volume of the 18% antifreeze must be .
In other words, the ratio of the volume of the 10% antifreeze to the volume of the 18% antifreeze must be  , or 0.6.
For example, you can take 3 liters of the 10% antifreeze and 5 liters of the 18% antifreeze.
Let's check it: , or 0.6.
For example, you can take 3 liters of the 10% antifreeze and 5 liters of the 18% antifreeze.
Let's check it: 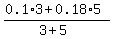 = = 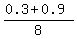 = = 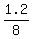 = 0.15. Correct.
Answer. The ratio of the volume of the 10% antifreeze to the volume of the 18% antifreeze must be = 0.15. Correct.
Answer. The ratio of the volume of the 10% antifreeze to the volume of the 18% antifreeze must be  , or 0.6. , or 0.6.
Solved.
For many other solved problems on liquid mixtures see the lessons
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Typical word problems on mixtures from the archive
- OVERVIEW of lessons on word problems for mixtures
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
|
|
|