SOLUTION: find the radius of a circle with center at (2,3), if the chord of length 10 is bisected at (-3,0)

Algebra ->  Length-and-distance -> SOLUTION: find the radius of a circle with center at (2,3), if the chord of length 10 is bisected at (-3,0)      Log On


   

Question 1045494: find the radius of a circle with center at (2,3), if the chord of length 10 is bisected at (-3,0)
Found 6 solutions by josgarithmetic, ikleyn, advanced_Learner, blaser211, MathTherapy, Edwin McCravy:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
I have not thought all the way through this yet nor done any calculations, but, do this: Find the equation of the line which contains the chord.

Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.
find the radius of a circle with center at (2,3), if the chord of length 10 is bisected at (-3,0)
~~~~~~~~~~~~~~~~~~~~ 

Make a sketch. Let the point O = (2,3) be the center of the circle.
Let the point B = (-3,0) bisects the given chord.
Let A and C be endpoints of this chord.

Then the triangle OAB is a right-angled triangle.

Its leg OB has the length 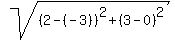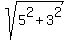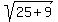sqrt%28%282-%28-3%29%29%5E2+%2B+%283-0%29%5E2%29 = sqrt%285%5E2+%2B+3%5E2%29 = sqrt%2825%2B9%29 = sqrt%2834%29 units.

Its leg AB has the length 10%2F2 = 5 units.

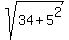Hence, the hypotenuse OA has the length sqrt%2834+%2B+5%5E2%29 = sqrt%2834+%2B+25%29 = sqrt%2859%29.

The hypotenuse OA is the radius of the circle.
Hence, the radius is sqrt%2859%29 units long.

Answer.  The radius is sqrt%2859%29 units long.

On properties of chords in a circle see the lessons
    - A circle, its chords, tangent and secant lines - the major definitions
    - The longer is the chord the larger its central angle is
    - The chords of a circle and the radii perpendicular to the chords
in this site.

In this site,  you have free of charge systematic and logically organized online textbook in Geometry
    - GEOMETRY - YOUR ONLINE TEXTBOOK.


Answer by advanced_Learner(501) About Me  (Show Source):
You can put this solution on YOUR website!
the radius is the distance from the centre to the point of interection
r=sqrt%28%282--3%29%5E2%2B%283-0%29%5E2%29
=sqrt%2834%29
equation is
%28x-2%29%5E2%2B%28y-3%29%5E2=34
graph confirms
.

Answer by blaser211(6) About Me  (Show Source):
You can put this solution on YOUR website!
sorry i in put the wrong problem...

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
find the radius of a circle with center at (2,3), if the chord of length 10 is bisected at (-3,0)
Length of perpendicular bisector from the center to the chord (one leg of right triangle with central angle as one of the vertices): sqrt%2834%29

Length of other leg of right triangle, with a value that is matrix%281%2C3%2C+%281%2F2%29%2C+of%2C+chord%29: 5 units

Length of radius (r), or hypotenuse of right triangle:

Answer by Edwin McCravy(20059) About Me  (Show Source):