Question 1045442: The orbit of a planet around a star is described by the equation (x^2/640,000)+(y^2/630,000) = 1 , wherein star is at one focus, and all units are in millions of kilometers. The planet is closest and farthest from the star, when it is at the vertices. How far is the planet when it is farthest from the star?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation 
Solution:
The ellipse has center at the 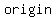 , and , and 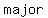 axis on the x-axis. axis on the x-axis.
if you compare  to to  , you see that , you see that
 , then , then  , so the vertices are , so the vertices are  is at ( is at (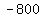 , ,  ) and ) and  is at( is at(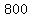 , ,  ). ).
Since  and and  , then , then




Suppose the star is at the focus at the right of the origin (this choice is arbitrary, since we could have chosen instead the focus on the left). Its location is then  ( ( , , ). ).
The 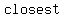 distance is then distance is then  (million kilometers) and the (million kilometers) and the 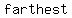 distance is distance is  (million kilometers). (million kilometers).
Answer:
 million km,the million km,the 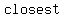 distance distance
and
 million km, the million km, the 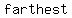 distance distance
|
|
|