SOLUTION: A set X with n(x)=525 is partitioned into subsets X_1, X_2, X_3, X_4, X_5, X_6. If n(X_1)=n(X_2)=n(X_3), n(X_4)=n(X_5)=n(X_6) and n(X_1)=6n(X_4), find n(X_1)

Algebra ->  Finite-and-infinite-sets -> SOLUTION: A set X with n(x)=525 is partitioned into subsets X_1, X_2, X_3, X_4, X_5, X_6. If n(X_1)=n(X_2)=n(X_3), n(X_4)=n(X_5)=n(X_6) and n(X_1)=6n(X_4), find n(X_1)      Log On


   

Question 1045405: A set X with n(x)=525 is partitioned into subsets X_1, X_2, X_3, X_4, X_5, X_6. If n(X_1)=n(X_2)=n(X_3), n(X_4)=n(X_5)=n(X_6) and n(X_1)=6n(X_4), find n(X_1)
Answer by ikleyn(52863) About Me  (Show Source):
You can put this solution on YOUR website!
.
A set X with n(x)=525 is partitioned into subsets X_1, X_2, X_3, X_4, X_5, X_6.
If n(X_1)=n(X_2)=n(X_3), n(X_4)=n(X_5)=n(X_6) and n(X_1)=6n(X_4), find n(X_1)
~~~~~~~~~~~~~~~~~~~~~ 

Let n(X_4) = n for brevity.


Then n(X_1) = n(X_2) = n(X_3) = 6n,

     n(X_4) = n(X_5) = n(X_6) =  n.

Hence, you have an equation

3n + 3*(6n) = 525,   or

21n = 525.

It implies n = 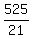525%2F21 = 25.

Then n(X_1) = 6n = 150.

Answer.  n(X_1) = 150.