Question 1045379: What is the equation of a parabola with vertex on the line y=x, axis parallel to Ox, and passing through (6,-2) and (3,4)?
Found 2 solutions by KMST, advanced_Learner:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the vertex be 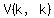 . .
The equation of a parabola with that vertex and axis parallel to the x-axis is
 . .
Substituting the coordinates of the given points, we have
 ---> --->
 ---> --->
Those two equations form a system of equation we have to solve to find  and and  . .
Subtracting one equation from the other, we have









Substituting the expression  for for  in in  we get we get
 --> --> --> -->
 --> -->
--> --> -->
The solutions to that equation are  and and  . .
Only one of those solutions should work, because
through any 3 points, (such as (6,-2) , (3,4), and 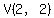 ) )
passes only one parabola with axis parallel to the x-axis.
Substituting  for for  in the original equation in the original equation
 , we get , we get
 ---> ---> ---> --->
The values  also satisfy equation also satisfy equation  . .
So,  is the equation of a parabola with vertex on the line is the equation of a parabola with vertex on the line  , axis parallel to the x-axis, and passing through (6,-2) and (3,4). , axis parallel to the x-axis, and passing through (6,-2) and (3,4).
The equation can be written in other, equivalent forms.
 <--> <--> <--> <-->
NOTE: The solution  does not yield the same a value when substituted in the two original equations. does not yield the same a value when substituted in the two original equations.
Answer by advanced_Learner(501)   (Show Source): (Show Source):
|
|
|