Question 1045345: Each of valves A,B and C when open release water into a tank at it's own constant rate.with all three valves open,the tank fills in 1 hr.with only valves A and C open,it takes 1.5 hr to fill the tank and with only valves B and C open,it takes 2 hr.How long does it take to fill the tank with valves A and B open?
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! A+B+C=1/1 of tank per hour
A+C=1/1.5 of tank per hour or 2/3
-A=C=-2/3
B=1-2/3=1/3 tank alone per hour
-------------------
A+B+C=1
-B-C=-1/2
A=1/2 tank alone per hour
------------------------
C=1/6 tank alone per hour , since they all add to 1.
----------------------
With A and B open, 5/6 of the tank is filled per hour.
That will require 6/5 hours or 72 minutes to fill with these two valves.
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Each of valves A,B and C when open release water into a tank at it's own constant rate.
With all three valves open,the tank fills in 1 hr. With only valves A and C open,it takes 1.5 hr to fill the tank and
with only valves B and C open,it takes 2 hr. How long does it take to fill the tank with valves A and B open?
~~~~~~~~~~~~~~~~~~~~~
Let "a" be the rate of the valve A in the " " unit.
Let "b" be the rate of the valve B in the same unit, and
Let "c" be the rate of the valve C in the same unit.
Then you are given
a + b + c = " unit.
Let "b" be the rate of the valve B in the same unit, and
Let "c" be the rate of the valve C in the same unit.
Then you are given
a + b + c =  = 1. (1)
a + c = = 1. (1)
a + c =  = =  , (2)
b + c = , (2)
b + c =  . (3)
We can rewrite this system in an equivalent form
2a + 2b + 2c = 2, (1)
a + c = . (3)
We can rewrite this system in an equivalent form
2a + 2b + 2c = 2, (1)
a + c =  , (2)
b + c = , (2)
b + c =  . (3)
Now distract both equations (2) and (3) from (1) (both sides). You will get
a + b = 2 - . (3)
Now distract both equations (2) and (3) from (1) (both sides). You will get
a + b = 2 -  - -  = = 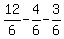 = =  .
The last equality says that the combined rate of the valves A and B is .
The last equality says that the combined rate of the valves A and B is  of the tank volume per hour.
Hence, the valves A and B will fill the tank in of the tank volume per hour.
Hence, the valves A and B will fill the tank in 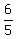 on an hour, or in 1 hour and 12 minutes working together. on an hour, or in 1 hour and 12 minutes working together.
On rate-of-work problems and specifically on joint-work problems see the lessons
- Rate of work problems
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Using quadratic equations to solve word problems on joint work
- Solving rate of work problem by reducing to a system of linear equations
- Selected joint-work word problems from the archive
- Joint-work problems for 3 participants
- OVERVIEW of lessons on rate-of-work problems
in this site.
|
|
|