Question 1045328: The sum of the lengths of any two sides of a triangle must be greater than the third side. If a triangle has one side that is 17 cm and a second side that is 4 cm less than twice the third side, what are the possible lengths for the second and third sides?
Found 3 solutions by Boreal, MathTherapy, ikleyn:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! second side is 2x-4
third side is x
17+x>2x-4; -x>-21;x<21
17+2x-4>x;x>-13
x+2x-4>17;3x>21, x>7
x>7 and <21
Check 8 and 20
8: sides are 17,8,12: 25>12,29>8, 20<17, it works.
20: sides are 17,20,36;17+20>36;17+36>20; 20+36>17, it works.
Try 6. It should not work
17,6,8: 6+8 is not >17
7
10<2x-4<22
Possible lengths would include 8 and 12; 20 and 36
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! The sum of the lengths of any two sides of a triangle must be greater than the third side. If a triangle has one side that is 17 cm and a second side that is 4 cm less than twice the third side, what are the possible lengths for the second and third sides?
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
The sum of the lengths of any two sides of a triangle must be greater than the third side.
If a triangle has one side that is 17 cm and a second side that is 4 cm less than twice the third side,
what are the possible lengths for the second and third sides?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the length o the third side.
Then the length of the second side is (2x-4).
According to the "triangle inequalities", these three inequalities should be in the place
17 + (2x-4) > x, (1)
(2x-4) + x > 17, (2)
17 + x > 2x-4. (3)
Inequality (1) is always valid and does not bring any restrictions.
Inequality (2) is x > 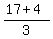 = 7.
Inequality (3) is x < 21.
Answer. The third side length must be between 7 and 21 (excluding the ends).
The second side must be longer than 7. In addition, the second side must be "4 cm less than twice the third side".
|
|
|
