|
Question 1045317: how can i find out the equation for ellipse when i have foci and length of major axis is given?
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You also need to know the coordinates of the center, and
what direction the major axis follows.
An ellipse is a stretched circle.
A circle of radius  with center at the origin has the equation with center at the origin has the equation
 <---> <--->  , ,
because  is the square of the distance from point (x,y) to origin (0,0) . is the square of the distance from point (x,y) to origin (0,0) .
Thankfully, we almost always get confronted by ellipses that are easier to calculate,
where the longest axis of symmetry, the major axis, is either
parallel to the x-axis (and we call it horizontal), or
parallel to the y-axis (and we call it vertical).
An ellipse with center at the origin and axes of symmetry parallel to the x- and y-axes has the equation
 or or  , with , with  . .
If the center of a circle, or ellipse is not  , ,
but a point 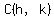 , ,
you just write 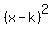 instead of instead of  ,and ,and
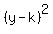 instead of instead of  . .
The distance  from each focus to the center, is related to from each focus to the center, is related to  and and  by by  , so you only need to know two of those distances. , so you only need to know two of those distances.
Given foci and length of major axis, you have  and and  , ,
just find  and plug the found and plug the found  value into the equation. value into the equation.
   . .
The points the farthest from the center are the vertices,
located on the major axis, at a distance  from the center. from the center.
The points the closest to the center are often called co-vertices,
located on the minor axis, at a distance  from the center. from the center.
The foci are located on the major axis, at a distance  to either side of the center. to either side of the center.
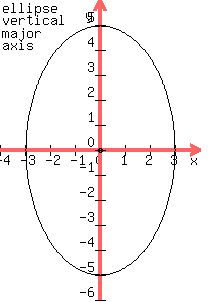
Here is an ellipse. you see the origin, point  . .
You see one labeled vertex, point 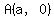 from the center. from the center.
I labeled the foci, focus 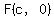 , and Focus , and Focus 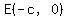 , ,
both at a distance  from the center. from the center.
I also labeled one of the co-vertices, point 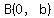 , at a distance , at a distance  from the center. from the center.
The fancy definition of ellipse says that for all the points on the ellipse,
the sum of the distances to one Focus and the other is the same.

You can see that point  is at a distance is at a distance 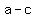 from focus from focus  , ,
and at a distance (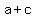 from focus from focus  . .
So the sum of the distance to the foci is
 for point for point  , and for all points in the ellipse. , and for all points in the ellipse.
Then, point  is at the same distance is at the same distance  from focus from focus  and focus and focus  . .
Applying the Pythagorean theorem to right triangle 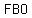 , ,
you get the relationship  . .
Answer by ikleyn(52879)   (Show Source): (Show Source):
|
|
|
| |