.
Please help me with this question
If  then the value of ab-c(2a+b) reduces to?
then the value of ab-c(2a+b) reduces to?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
You are given two equalities:
 =
=  , (1) and
, (1) and
 =
=  . (2)
From (1): a*ln(3) = b*ln(5), (3) and
From (2): b*ln(5) = c*ln(75) = c*(ln(3) + 2*ln(5)). (4). ( <--- since 75 =
. (2)
From (1): a*ln(3) = b*ln(5), (3) and
From (2): b*ln(5) = c*ln(75) = c*(ln(3) + 2*ln(5)). (4). ( <--- since 75 = 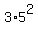 )
From (3), express ln(3) =
)
From (3), express ln(3) = 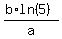 and substitute it into (4). You will get:
b*ln(5) =
and substitute it into (4). You will get:
b*ln(5) = 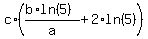 , or
ab*ln(5) = bc*ln(5) + 2ac*ln(5).
It implies
ab = bc + 2ac, or
ab - c*(2a + b) = 0.
Answer. ab - c*(2a + b) = 0.
, or
ab*ln(5) = bc*ln(5) + 2ac*ln(5).
It implies
ab = bc + 2ac, or
ab - c*(2a + b) = 0.
Answer. ab - c*(2a + b) = 0.