SOLUTION: Please help me find the solution & properties of ellipse and graph 4x^2=8y^2+8x-4y=8 Center: Vertices: Endpoints of minor axis: Foci:

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Please help me find the solution & properties of ellipse and graph 4x^2=8y^2+8x-4y=8 Center: Vertices: Endpoints of minor axis: Foci:      Log On


   

Question 1045034: Please help me find the solution & properties of ellipse and graph
4x^2=8y^2+8x-4y=8
Center:
Vertices:
Endpoints of minor axis:
Foci:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
It must be 4x%5E2%2B8y%5E2%2B8x-4y=8 , or something like that.
4x%5E2%2B8y%5E2%2B8x-4y=8--->4x%5E2%2B8x%2B8y%5E2-4y=8--->4%28x%5E2%2B2x%29%2B8%28y%5E2-%281%2F2%29%2Ay%29=8
When you look at that you realize that you almost have two squares:
4%28x%5E2%2B2x%2Bred%281%29%29=4%28x%2B1%29%5E2 and 8%28y%5E2-%281%2F2%29%2Ay%2Bgreen%281%2F16%29%29=8%28y%5E2-1%2F4%29%5E2 .
So, you add 4%2Ared%281%29%2B8%2Agreen%281%2F16%29=4%2B1%2F2 to both sides of the equal sign of the original equation to get
4x%5E2%2B8x%2B4%2B8y%5E2-4y%2B1%2F2=8%2B4%2B1%2F2
4%28x%5E2%2B2x%2B1%29%2B8%28y%5E2-%281%2F2%29%2Ay%2B1%2F16%29=25%2F2
4%28x%2B1%29%5E2%2B8%28y-1%2F4%29%5E2=25%2F2
At that point you realize that
since x and y only appear once,
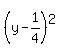and as %28x%2B1%29%5E2 and %28y-1%2F4%29%5E2 ,
the curve represented by that equation has vertical and horizontal axes of symmetry, given by
x%2B1=0 <---> x=-1 and
y-1%2F4=0 <---> y=1%2F4 .
So, the major and minor axes must be along those lines.
That means that the center is the point with highlight%28system%28x=-1%2Cy=1%2F4%29%29 .

You also realize that the ellipse cannot stray too far from that center.
The horizontal and vertical distance from the center to a point on the ellipse,
abs%28x%2B1%29 and abs%28y-1%2F4%29
have maximum possible values,
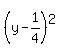because %28x%2B1%29%5E2 and %28y-1%2F4%29%5E2 have maximum possible values.

No matter what value y takes,
since %28y-1%2F4%29%5E2%3E=0 <---> 8%28y-1%2F4%29%5E2%3E=0 ,
4%28x%2B1%29%5E2=25%2F2-8%28y-1%2F4%29%5E2%3C=25%2F2 ,
and 4%28x%2B1%29%5E2%3C=25%2F2 means red%28%28x%2B1%29%5E2%3C=25%2F8%29 .
so there are horizontal ends to the ellipse.
Similarly, no matter what value x takes,
there are vertical ends to the ellipse
Since %28x%2B1%29%5E2%3E=0 <---> 4%28x%2B1%29%5E2%3E=0 ,
8%28y-1%2F4%29%5E2=25%2F2-4%28x%2B1%29%5E2%3C=25%2F2 ,
and 8%28y-1%2F4%29%5E2%3C=25%2F2 <---> green%28%28y-1%2F4%29%5E2%3C=25%2F16%29 .
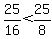Since 25%2F16%3C25%2F8 ,
the ellipse stretches farther in the horizontal) x-direction.
That means that the horizontal y=1%2F4 axis is the major axis.

The ends of the ellipse along the major axis are the vertices.
Their distance to the center is the semi-major axis, a , given by
red%28%28x%2B1%29%5E2%3C=25%2F8=a%5E2%29 <--> abs%28x%2B1%29%5E2%3C=sqrt%2825%2F8%29=sqrt%2825%2A2%2F16%29=5sqrt%282%29%2F4 .
So, the vertices have
x%2B1=-5sqrt%282%29%2F4 <--> highlight%28x=-1-5sqrt%282%29%2F4%29 <--> highlight%28x=%28-4-5sqrt%282%29%29%2F4%29 and
x%2B1=5sqrt%282%29%2F4 <--> highlight%28x=-1%2B5sqrt%282%29%2F4%29 <--> highlight%28x=%28-4%2B5sqrt%282%29%29%2F4%29 ,
along with highlight%28y=1%2F4%29 .

The minor axis, along the line x=-1%29 , has ends at a distance b from the center.
That distance is called the semi-minor axis and is given by
green%28%28y-1%2F4%29%5E2%3C=25%2F16=b%5E2%29 <---> abs%28y-1%2F4%29%3C=sqrt%2825%2F16%29 <---> abs%28y-1%2F4%29%3C=5%2F4 .
So, the ends of the (vertical) minor axis of symmetry of the ellipse have
y=1%2F4-5%2F4=highlight%28-1%29 and y=1%2F4%2B5%2F4=highlight%283%2F2%29 ,
along with highlight%28x=-1%29 .

The foci of the ellipse are along the major axis, y=1%2F4%29 ,
at a distance c from the center of the ellipse,
and we know that a%5E2=b%5E2%2Bc%5E2 .
Substituting the values found before,
red%2825%2F8=a%5E2%29 and green%28%28y-1%2F4%29%5E2%3C=25%2F16=b%5E2%29 , we get
25%2F8=25%2F16%2Bc%5E2 ---> c%5E2=25%2F8-25%2F16 ---> c%5E2=50%2F16-25%2F16 ---> c%5E2=25%2F16 ---> c=sqrt%2825%2F16%29 ---> c=5%2F4 .
So, the coordinates for the foci are highlight%28y=1%2F4%29 , along with
x=-1-5%2F4=-4%2F4-5%2F4=highlight%28-9%2F4%29 for one focus, and
x=-1%2B5%2F4=-4%2F4%2B5%2F4=highlight%281%2F4%29 for the other focus.