Question 1044876: Asking this question again as was responded too but no answer was given:
Need to find the surface area of composite figures and leave answer in terms of pi. The first figure is a cone with a radius of 10mm and a height of 24mm (does not give the slant height) and inside is a hemisphere with a radius of 8mm.
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The reason there was no answer is because of the words "and inside is a hemisphere with a radius of 8mm."Surface area problems are always about "outside" things
only, and never involve "inside" things.
Edwin
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a right circular cone, the base radius,  is perpendicular to the height, is perpendicular to the height,  . .
Radius, height, and slant height form a right triangle,
and the slant height can be calculated using the Pythagorean theorem as
 . .
So, when given  and and  , the lateral surface area of a right circular cone can be calculated as , the lateral surface area of a right circular cone can be calculated as
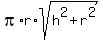 . .
With  and and  , ,
the slant height is  , ,
and the lateral surface area is  . .
I assume that your composite figure is a cone with a hemisphere taken out of the base, so that the cross section looks like this:
 , and only a ring is left of the base of the cone,like this: , and only a ring is left of the base of the cone,like this:  . .
The surface area of that ring that is left over of the base of the cone
is the area of a circle of radius 
minus the area of a circle of radius  ; ;
 . .
The surface area of a sphere of radius  is is  , ,
so the surface of a hemisphere of radius  is is
 , ,
The surface area of your composite figure is mad of three parts:
lateral surface area of the cone =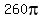 , ,
area of ring on the cone base =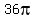 , and , and
area of hemisphere = . .
Total surface area = . .
|
|
|