|
Question 1044782: Please help me solve this equation
Find the Parabola properties and graph
y^2+6x+6y=39
Vertex:
Focus:
Directrix:
Axis of symmetry:
Endpoints of latus retum:
Found 2 solutions by MathLover1, solver91311:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the Parabola properties and graph
given:

Vertex:
first write your equation in vertex form  (since y squared) where (since y squared) where  and and  are are  and and  coordinates of the vertex coordinates of the vertex









 and and 
vertex is at (  , ,  ) )
Since the value of a is negative, the parabola opens left.
Focus:
The focus of a parabola can be found by adding p to the x-coordinate h if the parabola opens left or right.
( , , ) )
Find p, the distance from the vertex to the focus.
Find  , the distance from the vertex to a focus of the parabola by using the following formula. , the distance from the vertex to a focus of the parabola by using the following formula.

since  , we have , we have



(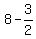 , , ) )
(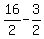 , , ) )
( 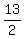 , ,  )->focus )->focus
Directrix:
The directrix of a parabola is the vertical line found by subtracting p from the x-coordinate h
of the vertex if the parabola opens left or right.




Axis of symmetry:
Find the axis of symmetry by finding the line that passes through the vertex and the focus.
vertex is at (  , ,  ) )
( 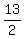 , ,  )->focus )->focus
and that will be 
Endpoints of latus retum:
length of latus rectum = 
endpoints of the latus rectum: ( , , ) and ( ) and ( , ,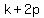 ) )
since  , ,  and and  we have we have
(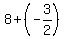 , ,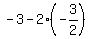 ) and ( ) and (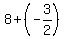 , ,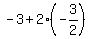 ) )
(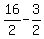 , ,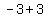 ) and ( ) and (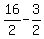 , , ) )
(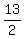 , , ) and ( ) and (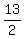 , , ) )

Answer by solver91311(24713)   (Show Source): (Show Source):
|
|
|
| |