SOLUTION: Please give the corresponding equations in rectangular coordinates? 1) r = &#960; 2) &#952; = 6 3) r = 4/(3cos&#952; -sin&#952; ) 4) r^2 = 36/(9-13sin^2(&#952;) )

Click here to see ALL problems on Trigonometry-basics

Question 1044706: Please give the corresponding equations in rectangular coordinates?
1) r = π
2) θ = 6
3) r = 4/(3cosθ -sinθ )
4) r^2 = 36/(9-13sin^2(θ) )
Found 2 solutions by ikleyn, advanced_Learner:
Answer by ikleyn(52909) (Show Source):
You can put this solution on YOUR website!
.
Please give the corresponding equations in rectangular coordinates?

1) r = . <--- = , or = 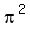. It is the circle of the radius centered at (0,0). 2) = 6. <--- = tan(6), where tan(6) is the tangent of 6 radians (which is slightly less than 360 degs = = 6.28 . . . ) In addition, y < 0, x > 0, since the angle is in QIV (fourth quadrant). So, it is the ray in the QIV. 3) r = 4/(3cosθ -sinθ ) 4) r^2 = 36/(9-13sin^2(θ) )

Comment from student: Your answer in #2 is only partly correct. My calculus book says it is only y = (tan6)x.

My response: Thank you for your feedback.
My answer is fully correct.
Your calculus book is only partly correct.
The set of points = 6 is the ray starting at the origin of the coordinate system.
It is not a straight line.

Answer by advanced_Learner(501) (Show Source):
You can put this solution on YOUR website!
.

SOLUTION: Please give the corresponding equations in rectangular coordinates? 1) r = &#960; 2) &#952; = 6 3) r = 4/(3cos&#952; -sin&#952; ) 4) r^2 = 36/(9-13sin^2(&#952;) )

SOLUTION: Please give the corresponding equations in rectangular coordinates? 1) r = π 2) θ = 6 3) r = 4/(3cosθ -sinθ ) 4) r^2 = 36/(9-13sin^2(θ) )