Question 1044580: solve for x:
2x^5+17x^4+46x^3+31x^2-36x-36=0
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Rational Roots Theorem, to factorize as much as possible to find the roots (which will show solutions).
The equation has potentially, five roots. Degree is five. Possible roots to check should be or include the pluses and minuses of 1, 2, 3, 4, 6, 9, 12, 18, and maybe 36.
-
First check for -1 and -3.
-3 | 2 17 46 31 -36 -36
|
| -6 -33 -39 24 36
|__________________________________
2 11 13 -8 -12 0
|
-1 | 2 11 13 -8 -12
| -2 -9 -4 12
|__________________________________
2 9 4 -12 0
-3 again | 2 9 4 -12
|
| -6 -9 15
|__________________________
2 3 -5 3
-1 again | 2 9 4 -12
|
| -2 -7 3
|__________________________
2 7 -3 -9
What about -2?
-2 | 2 9 4 -12
|
| -4 -10 12
|______________________________
2 5 -6 0
This gives the factorization to  , and quadratic formula solution should give the last two roots (but it is also factorable).
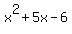
Completely factored equation:
Solution set for the equation is {-1,-2, -3, -6, 1}.
|
|
|
